Принцип ориентирования по полю двигателя при частотном управлении
Координатные и фазные преобразования переменных, рассмотренные в гл. 2, в настоящее время не только используются для упрощения анализа динамических процессов электромеханического преобразования энергии, но и успешно применяются в качестве математической основы построения алгоритмов функционирования систем управления электроприводами переменного тока. В частности, этот математический аппарат является основой принципа ориентирования по полю двигателя, который реализован в ряде совершенных систем частотного управления асинхронными и синхронными электроприводами.
Для пояснения этого принципа предположим, что при управлении двигателем доступны для измерения текущие значения модуля, угловой скорости и фазы вектора потокосцепления ротора. Тогда ось х синхронно вращающейся системы координат х, у представляется возможным совместить с мгновенным направлением этого вектора:
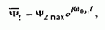
при этом Y2x=Y2max, Y2y=0 вектор тока статора становится ориентированным относительно

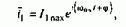
его проекция на ось х i1x является мгновенным значением намагничивающего тока машины, а проекция на ось у, как было показано в §6.5 для статического режима, представляет собой активный ток статора. Основой для вычисления текущих переменных служат уравнения механической характеристики в осях х, у (wk=w0эл), ориентированных по полю двигателя, в которых Y2x=Y2max, Y2y=0 в любой момент времени:

С помощью уравнений потокосцеплений при ориентировании по вектору


где



Полученные уравнения наглядно представляют динамические особенности асинхронного электропривода с частотным управлением при ориентировании по полю двигателя. Изменением i1х можно регулировать потокосцепление ротора, но при существенных проявлениях электромагнитной инерции, характеризуемой большими постоянными времени Т1 и Т2 При постоянном потоке (Y2max=const) система (8.102) представляется в виде

при этом электромагнитная инерция обусловлена только изменениями потоков рассеяния статора (малая постоянная времени T1s) и полностью проявляется только при питании статора от источника напряжения. Если преобразователь частоты обладает свойствами источника тока, при Y2max=const теоретически асинхронный двигатель представляет собой безынерционный объект управления, а при регулировании потока по отклонению его механическая характеристика определяется уравнениями

Отсюда следует, что, если при управлении асинхронным двигателем оперировать в цепях управления не с реальными переменными машины, а с преобразованными к координатным осям, ориентированным по полю, можно отдельно управлять магнитным потоком и моментом двигателя, имея дело не с переменными синусоидальными величинами, а с постоянными их преобразованными значениями. Это позволяет строить систему управления асинхронным двигателем аналогично системе управления двигателем постоянного тока. Основой построения таких систем является информация о мгновенном значении и пространственном положении вектора потокосцепления в воздушном зазоре, непосредственное измерение которого обычно осуществляется с помощью датчиков Холла.
В соответствии с изложенным для реализации управления потоком и моментом двигателя по отклонению необходимо измерить мгновенные реальные трехфазные токи статора и поток в воздушном зазоре, осуществить преобразование трехфазных переменных к эквивалентным двухфазным и произвести координатное преобразование их к осям, ориентированным по полю. Определенные таким образом преобразованные текущие значения i1x и i1y остается сравнить с их заданными значениями, получить сигналы управления потоком и моментом в осях х, у, а затем осуществить обратные координатное и двухфазно-трехфазное преобразования и получить действительные сигналы для управления трехфазным преобразователем частоты. Для осуществления этой цепочки операций необходимо управляющее вычислительное устройство, некоторые особенности которого можно установить, рассматривая схему, приведенную на рис.8.37,a.
Система управления состоит из трех крупных блоков: блока вычисления текущих значений переменных БВТП, блока регуляторов переменных БРП и блока вычисления заданных значений переменных - управляющих воздействий БВЗП. Рассмотрим назначение, основные элементы и особенности измерительного блока БВТП.
Для того чтобы вычислить амплитуду и фазу переменной трехфазного двигателя, достаточно измерить мгновенные значения этой переменной в двух фазах двигателя. Блок БВТП преобразует измеренные с помощью датчиков Холла трехфазные мгновенные значения потока в воздушном зазоре Yma и Ymb и измеренные с помощью датчиков тока действительные трехфазные переменные токи i1a и i1b в ориентированные по полю значения потокосцепления ротора Y2mах намагничивающего тока i1х и активного тока i1y. Он состоит из блоков фазных преобразований БФП1 и БФП2, блока векторного фильтра БВФ и блока координатного преобразования БКП2 Блок БФП1 осуществляет трехфазно-двухфазное преобразование потокосцепления в воздушном зазоре в соответствии с формулами (2.34).

Кроме того, блок БФП1 вычисляет необходимое для контроля потокосцепление ротора в соответствии с формулами

Необходимые для решения (8.106) значения i1a и i1b вычисляются блоком БФП2 по формулам, аналогичным (8.105). Так как переменные Y2a и Y2b вычислены с помощью (8.106) через переменные статора, они представляют собой синусоидальные величины, изменяющиеся с частотой w0эл.
Блок векторного фильтра БВФ решает задачу определения мгновенного пространственного угла поворота w0эл вектора потокосцепления ротора


Так как Y2a=Y2max·cos fоэл и Y2b=Y2max· sin ф0эл, то, подставив эти выражения в (8.107), после преобразований получим

Нетрудно видеть, что на выходе блока БКП1 получаются составляющие вектора

При отсутствии в кривой потока высших гармоник в установившемся режиме благодаря интегральной составляющей регулятора РФ достигалось бы полное устранение ошибки Dф0эл=0. При этом f'0эл=f0эл и в соответствии с (8.108) Y2u=Y2max, a Y2v=0. Таким образом, составляющая Y2v непосредственно связана со знаком ошибки Df0ЭЛ и ее значением. С помощью задающего сигнала Dф0элз устанавливается минимальное значение ошибки, обусловленной гармониками потока.
Полученные на выходе БВФ функции cos ф0эл и sin ф0эл используются для координатного преобразования токов i1a и i1b, которое осуществляется блоком БКП2. Этот блок не имеет отличий от блока БКП1 (рис.8.37,б); на его выходе получаются составляющие тока статора i1х и i1y, постоянные по значению (для статического режима). Эти значения, а также текущие значения потокосцепления Y2mах и скорости w поступают в блок регуляторов переменных БРП и используются для регулирования по отклонению от заданных значений.
Поступающие на вход блока регуляторов БРП задающие сигналы Y2maxз и w3, совместно с ориентированными по полю текущими значениями переменных используются для вычисления заданных значений переменных i1хз и i1yз, с помощью которых блок вычисления задающих сигналов БВЗП формирует синусоидальные напряжения управления преобразователем u1aз, u16з и u1сз.
Здесь для пояснения принципа ориентирования по полю подробно рассмотрен блок вычисления текущих переменных БВТП системы «Трансвектор», разработанной фирмой «Сименс» (ФРГ) для управления асинхронными и синхронными электроприводами с частотным управлением.Описание других блоков этой системы приведено в [4].
Регулирование скорости двигателя
При рассмотрении свойств двигателя постоянного тока как объекта управления в гл.3 были выявлены возможности управления процессами электромеханического преобразования энергии по двум каналам: по цепи якоря и по цепи возбуждения двигателя. В предшествующем изложении вопросы регулирования момента и скорости этого вида электропривода рассматривались при постоянстве магнитного потока двигателя Ф=Фном=const либо при постоянстве тока якоря /я=const, Ф=var в системе источник тока - двигатель.
Практически возможность регулирования скорости путем воздействия на поток двигателя используется широко в разомкнутых системах электроприводов, получающих питание от сети постоянного тока (Uс=UHOM=const), в замкнутых системах Г-Д и ТП-Д с так называемым двухзонным регулированием скорости, а также в электроприводах по системе ИТ-Д, замкнутых по цепи возбуждения двигателя отрицательной обратной связью по скорости. В связи с этим способ регулирования скорости изменением магнитного потока имеет важное значение, и его особенности заслуживают самостоятельного рассмотрения.

Уравнения статических электромеханической (3.9) и механической (3.10) характеристик для анализа влияния изменений потока двигателя удобно записать в виде

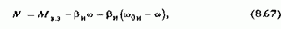
где Iкз=UHOM/RяS - ток короткого замыкания якорной цепи при номинальном напряжении; Мкз=kФIКЗ- момент короткого замыкания; w0и=Uном/kФ - скорость идеального холостого хода искусственной характеристики, соответствующей различным значениям потока; bи=k2Ф2/RяS - модуль статической жесткости, соответствующий различным значениям потока при Rдобя=0.
Так как в номинальном режиме магнитная цепь двигателя насыщена, возможности увеличения потока сверх номинального незначительны и практического интереса не представляют. Исходя из этого обмотка возбуждения двигателя рассчитывается по нагреву на ток возбуждения, необходимый для получения номинального потока. Поэтому регулировать поток можно только в сторону уменьшения - ослабления поля двигателя.
Статические характеристики двигателя при регулировании потока показаны на рис.8.25. Электромеханические характеристики при различных значениях потока в соответствии с (8.66) пересекаются в точке w=0, Iя=Iкз (рис.8.25,a). Механические характеристики в связи с уменьшением момента Мкз в (8.67), пропорциональным уменьшению потока, пересекаются в двигательном режиме (рис.8.25,б), причем точка пересечения с естественной характеристикой по мере уменьшения потока перемещается в сторону меньших моментов. Однако при реальных пределах ослабления поля и при нагрузках, не превышающих номинальную, скорость двигателя при ослаблении поля возрастает, как это показано для номинального момента Мном на рис.8.25,б.

В отличие от всех выше рассмотренных способов регулирования скорости при ослаблении поля регулирование осуществляется при изменяющемся потоке, что определяет принципиально иную зависимость допустимой нагрузки от скорости.
Если принять в качестве критерия допустимой нагрузки ток Iя=Iном, то допустимый момент при регулировании определится соотношением

которое показывает, что при ослаблении поля нагрузку на валу двигателя необходимо снижать. Выразив из (8.66) скорость при Iя=Iном и подставив это выражение в (8.68), получим

где Рэном - номинальная электромагнитная мощность двигателя.
Умножив (8.69) на w, получим следующее условие допустимой нагрузки:


На рис.8.26 приведены зависимости Mдоп=f(w) и Pдоп=f(w) в диапазоне изменений скорости двигателя с независимым возбуждением, обеспечиваемом всеми рассмотренными способами регулирования его скорости. Реостатное регулирование и регулирование напряжением якорной цепи осуществляются в пределах 0¸wном при постоянном моменте и линейно возрастающей мощности. Ослабление поля охватывает зону w>wном и осуществляется при постоянной мощности Р=Рном=const и допустимом моменте, изменяющемся обратно пропорционально скорости (8.69).
Небольшая мощность цепи возбуждения определяет относительно небольшие габариты, массу и стоимость регулировочного реостата Rдоб.в, что позволяет получить достаточно высокую плавность регулирования. Простота, экономичность данного способа регулирования и благоприятные регулировочные характеристики определяют его широкое использование на практике. Рассмотрим, как влияет ослабление поля на динамические характеристики привода. Динамическая жесткость механической характеристики при ослаблении поля выражается соотношением

Амплитудно-частотные характеристики динамической жесткости |bдин|=f(W) во всем диапазоне частот имеют модуль жесткости, снижающийся при ослаблении поля, а ФЧХ при этом не изменяется. Передаточная функция двигателя имеет вид

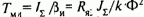
Рассматривая (8.72), можно установить, что при ослаблении поля двигателя вследствие увеличения электромеханической постоянной Тм.и соотношение постоянных времени изменяется в сторону снижения показателя колебательности и увеличения коэффициента демпфирования переходных процессов.
При большом моменте инерции механизма и значительном ослаблении поля электромагнитные переходные процессы могут протекать замедленно.
Для механизмов, момент нагрузки которых при регулировании скорости изменяется так, что мощность остается примерно постоянной, ослабление поля двигателя постоянного тока с независимым возбуждением является лучшим способом регулирования скорости. Именно этим объясняется разработка специальных серий двигателей, рассчитанных на глубокое ослабление поля. На основе их применения реализуются наиболее простые системы регулирования скорости в сравнительно широком диапазоне (до D=8), в которых для управления пуском двигателя используется ступенчатое реостатное регулирование пускового тока и момента двигателя. При этом, если по технологическим условиям требуется более высокая стабильность заданной скорости электропривода, чем обеспечиваемая жесткостью bи в разомкнутой системе, для увеличения точности регулирования могут использоваться системы автоматической стабилизации скорости, замкнутые отрицательной обратной связью по скорости, воздействующей на напряжение возбуждения двигателя.
Для осуществления автоматического регулирования по отклонению необходимо осуществить питание обмотки возбуждения двигателя от усилителя мощности, например от тиристорного возбудителя. Принципиальная схема автоматического регулирования скорости воздействием на цепь возбуждения двигателя показана на рис.8.27,а. Уравнения, описывающие работу этой схемы, если полагать характеристику намагничивания двигателя линейной и однозначной и пренебречь влиянием вихревых токов в стали магнитопровода, имеют вид

Вследствие того что регулирование осуществляется изменением потока двигателя, система (8.73) является нелинейной. Для решения задачи оптимизации данной схемы регулирования скорости методом последовательной коррекции необходимо ее линеаризовать. Полагая индуктивность Lя пренебрежимо малой и принимая Мc=0 при Uя=Uном=const, получаем

где Duу, Duв, DФ и Dw - малые отклонения переменных от точки статического равновесия, определяемой значениями соответственно Uy°, Uв°, Ф° и w°; T°ми=JSRяS/k2Ф02 - электромеханическая постоянная двигателя при Ф=Ф°.


Для настройки на технический оптимум необходимо получить оптимальную передаточную функцию разомкнутого контура в виде

Разделив (8.76) на (8.75), определим передаточную функцию регулятора скорости:

Таким образом, для одноконтурной системы регулирования скорости и в данном случае необходим ПИД-регулятор. Благодаря наличию интегральной составляющей в (8.77) система обеспечивает астатическое регулирование скорости как по управляющему, так и по возмущающему воздействиям, а динамическая точность и быстродействие определяются значением 2Tm. При этом неучтенная выше малая постоянная Тя может быть учтена увеличением суммарной некомпенсируемой постоянной контура Tm=Tтв+Tя.
Однако в данном случае в связи с нелинейностью системы оптимальная настройка сохраняется в ограниченных пределах отклонений переменных от принятой при линеаризации точки астатического равновесия w0, Ф°. Если полагать характеристику намагничивания двигателя линейной, в структурной схеме на рис.8.27,б нелинейность заключена в электромеханической постоянной T°ми. Как было показано, в разомкнутой системе ослабление поля приводит к увеличению Тм.и, соответствующему возрастанию демпфирования, и к некоторому увеличению длительности процессов.
При переходе к замкнутой системе регулирования исходную точку для оптимизации также необходимо выбрать так, чтобы изменения потока при регулировании вызывали увеличение демпфирования контура, а не его ослабление и связанное с этим ухудшение качества регулирования. Так как условия компенсации постоянной TВ при линейной характеристике намагничивания от изменений потока не зависят, с учетом (8 77) передаточную функцию разомкнутого контура можно записать в виде

где

Из рассмотрения (8.78) следует, что для выполнения поставленного выше условия необходимо в качестве расчетной точки для оптимизации выбирать режим, где Тк.рaсч и Тм.и.расч максимальны. Таким режимом является работа при минимальном потоке двигателя. При этом оптимальное соотношение постоянных контура будет иметь место только при максимальной скорости, а по мере усиления поля в соответствии с (8.78) оно изменяется в сторону увеличения демпфирования динамических процессов.
При автоматическом регулировании скорости в схему на рис 8.27 для ограничения тока при пусках и торможениях в цепь якоря вводятся пусковые сопротивления, как и в схеме на рис.8.24, а зона регулирования скорости располагается выше естественной характеристики w>wном . Диапазон регулирования скорости при этом ограничен допустимыми пределами ослабления поля (D< 8), поэтому во многих случаях прибегают к двухзонному регулированию скорости, при котором ослабление поля сочетается с регулированием подведенного к якорной цепи напряжения uя=var по системе Г-Д или ТП-Д. Наиболее простые системы управления при двухзонном регулировании реализуются при питании якорной цепи от источника тока В качестве полноуправляемого источника тока может быть использован тири-сторный преобразователь с быстродействующим контуром регулирования тока якоря, а при работе в двигательном режиме простым и надежным решением является использование индуктивно-емкостного преобразователя (см. §7.3).
При использовании нерегулируемого индуктивно-емкостного преобразователя схеме электропривода (рис.8.28,a) соответствует следующая система дифференциальных уравнений:

Уравнениям (8.79) соответствует структурная схема, приведенная на рис.8.28,б. С помощью (8.79), полагая Tтв»0, получаем уравнение динамической механической характеристики

Отсюда динамическая жесткость механической характеристики определяется соотношением

Таким образом, при безынерционном преобразователе электропривод по схеме рис.8.28,а обладает механической характеристикой, аналогичной характеристике двигателя с независимым возбуждением при Uя=const, однако отличается значительно большей инерционностью цепи формирования момента, так как Тк>>Тя.
Передаточная функция разомкнутого контура регулирования скорости в соответствии с рис 8.28,б имеет вид

где Tми=JS/bзам - электромеханическая постоянная электропривода на искусственной характеристике.
Сопоставляя (8.81) с (4.12), можно прийти к выводу, что при одинаковых модулях жесткостей характеристик в разомкнутой системе УП-Д и в замкнутой системе ИТ-Д соотношение постоянных Тм и и Тв оказывается значительно менее благоприятным, чем соотношение постоянных Тм и Тя двигателя. Для получения удовлетворительного качества регулирования приходится ограничивать коэффициент обратной связи значениями, при которых жесткость рабочего участка механических характеристик оказывается невысокой, либо вводить корректирующие обратные связи.
Примерный вид характеристик показан на рис.8.29,а. При их построении учтено, что напряжение возбудителя UBmax в a=2¸4 раза превышает номинальное напряжение возбуждения двигателя для форсирования переходных процессов. Поэтому обратная связь по скорости поддерживает скорость постоянной только в пределах линейного участка характеристики возбудителя, в конце которого ток возбуждения значительно превышает номинальный и с учетом насыщения магнитной цепи двигателя устанавливается поток, превышающий номинальный на 10-30%. Соответственно пусковой момент, как показано на рис.8.29,а, составляет (1,1-1,3)МНОМ.


Если по техническим требованиям желательно получение мягких характеристик, аналогичных характеристикам двигателя с последовательным возбуждением, можно использовать обратную связь по ЭДС двигателя. При этом уравнение статических характеристик имеет следующий вид:

где k0э - коэффициент обратной связи по ЭДС.
Этому уравнению соответствуют нелинейные механические характеристики, которые показаны на рис 8.29,б.

Наличие в контуре регулирования большой постоянной времени обмотки возбуждения определяет целесообразность использования последовательной коррекции. При указанном выше значительном запасе по напряжению возбуждения (а=2-^-4) полезно ввести ограничение максимального тока возбуждения в переходных процессах допустимым значением, а это наиболее удобно обеспечивается введением подчиненного контура регулирования тока возбуждения, как показано на рис.8.30.
Передаточную функцию объекта регулирования тока возбуждения, если допустимо пренебречь влиянием вихревых токов и отнести инерционность тиристорного возбудителя к некомпенсируемой Тm=Tт.в, можно записать в виде

Для получения оптимальной передаточной функции этого контура необходима следующая передаточная функция регулятора тока возбуждения:

Таким образом, регулятор тока возбуждения должен иметь передаточную функцию интегрально-пропорционального звена. Передаточная функция объекта регулирования скорости состоит из передаточной функции замкнутого контура тока, которую упростим, отбросив в знаменателе член второго порядка, и передаточной функции механического звена:

Регулятор скорости должен иметь передаточную функцию

пропорционального звена.
Синтезированная система регулирования скорости в пределах допустимой линеаризации характеристик ее элементов обладает статическими и динамическими свойствами однократно интегрирующей системы, подробно рассмотренными ранее. Выражение динамической жесткости механической характеристики, справедливое для линейного участка характеристики регулятора скорости, показанной на рис.8.30, имеет вид

Модуль статической жесткости
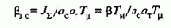
совпадает с (8.44), несмотря на принципиально иное построение системы электропривода и другое выражение динамической жесткости bДИН(p). Следовательно, по статической и динамической точности регулирования инерционная система управления по каналу потока оказывается в результате последовательной коррекции равноценной быстродействующей системе ТП-Д. Однако этот результат не должен ввести в заблуждение: как было отмечено для системы Г-Д, большая инерционность обмотки возбуждения ограничивает реально достижимое быстродействие целесообразным завышением мощности возбудителя.
Допустим, время регулирования тока возбуждения при стандартной настройке линейного контура регулирования составляет около 5Tm=0,05 с. Если постоянная времени цепи возбуждения Тв=2,5 с, то для достижения номинального значения тока за время tв=0,05 с необходим следующий коэффициент форсирования:
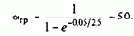
Для реализации такого коэффициента форсирования необходимо завысить мощность в 50 раз, и по габаритам возбудитель может оказаться больше двигателя, что явно нецелесообразно. При использовании современных быстродействующих и компактных тиристорных возбудителей приемлемые значения коэффициентов форсирования не превосходят a=10. В рассматриваемом примере достижимое время возбуждения двигателя от Iв=0 до Iв=Iв.ном

Соответственно время нарастания момента в системе ИТ-Д при таких параметрах при номинальном скачке задания скорости определяется не коэффициентом обратной связи по скорости, а заложенным при проектировании запасом по напряжению возбуждения
Для механизмов, требующих повышенной плавности переходных процессов, достигаемой ограничением темпа нарастания момента (dM/dt)£(dM/dt)дoп или рывка r=d2w/dt2<rдоп, полученное быстродействие может быть вполне достаточным Однако для механизмов, требующих весьма высокого быстродействия, управление по каналу возбуждения необходимо сочетать с управлением по более быстродействующему каналу цепи якоря
Реостатное регулирование момента
Значения момента М и скорости w при данной нагрузке Мс на каждом этапе работы электропривода определяются его механической характеристикой. Изменяя параметры и воздействия, от которых зависит механическая характеристика, можно изменять в требуемом направлении момент, развиваемый двигателем при данной скорости, и таким образом регулировать момент электропривода, а также связанные с ним ток силовой цепи и ускорение движущихся масс системы.
Анализируя уравнение статической механической характеристики обобщенного двигателя с линейной механической характеристикой
М=b(w0-w), (7.1)
можно заключить, что при данных параметрах отклонения момента от требуемого значения тем больше, чем выше модуль жесткости b. Иными словами, при регулировании момента электромеханическая связь является сильным возмущением, и с точки зрения регулирования момента наиболее эффективны изменения параметров, позволяющих неограниченно уменьшать модуль статической жесткости b. Таким параметром является сопротивление якорной (роторной) цепи двигателя.
Схемы реостатного регулирования момента и тока представлены на рис.7.1,а и б. На рис.7.1,е построены естественная характеристика М=f(w) (прямая 1) и реостатная характеристика 2, соответствующая определенному добавочному резистору в силовой цепи. Точность регулирования момента при характеристике 2 определяется при заданных пределах изменения скорости электропривода Dwmax=wmax-wmin соотношением

Следовательно, при этих условиях относительная точность регулирования момента остается при увеличении Rдоб неизменной, а абсолютные ошибки уменьшаются.
Практически требуется при широких пределах изменения скорости (пуск, реверс) поддерживать изменения момента и тока в заданных пределах от Мmаx=М1 до Мmin=М2 (Imax=I1, Imin=I2).
Для выполнения этого условия требуется ступенчатое или плавное изменение /?доб по мере изменения скорости.

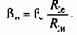
где RSе - суммарное сопротивление силовой цепи на естественной характеристике; RSи- то же при введении Rдоб, при этом
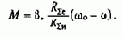
откуда при М=М,=const
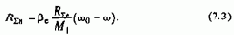

Аналогичные характеристики справедливы и для двигателя с последовательным возбуждением для токов якоря I1=const и I2=const (рис.7.2,б).
Графики на рис.7.2 позволяют наглядно оценивать число ступеней регулировочного резистора Rдоб, необходимое для поддержания момента и тока в заданных пределах во время пуска электропривода. Неизменное сопротивление RSи=R1=const обеспечивает поддержание момента в пределах М2<М<М1 при изменениях скорости от 0 до w1 (прямые 7 и 8). При дальнейшем увеличении скорости w>w1 выводится первая ступень резистора R1 и суммарное сопротивление уменьшается до RSи=R2 (прямые 9 и 6) и т. д.
Зависимости RSи=f(w) при М=const (I=const) используются для расчета пусковых сопротивлений, особенно для двигателей с последовательным возбуждением. Значения ступеней сопротивления определяются, как показано на рис.7.2. Одинаковость бросков тока при переключениях Iя=I1 при этом обеспечивается подбором значения I2(М2). Диапазон реостатного регулирования момента и тока ограничен сверху перегрузочной способностью двигателя, а пределы изменения скорости, в которых можно получить заданную точность регулирования, уменьшаются с ростом р, т. е. по мере уменьшения Rдоб. Плавность реостатного регулирования момента и тока в разомкнутой системе невелика. В связи с необходимостью переключений в силовой цепи двигателя получение большего числа ступеней реостата связано с увеличением габаритов коммутирующего устройства.
Однако имеются примеры, когда при высокой требуемой точности регулирования момента в переходных процессах пуска и торможения предусматривают значительное число ступеней реостата и соответствующее увеличение размеров и стоимости станций управления. При этом увеличение габаритов и стоимости станций управления окупается простотой и надежностью данного способа регулирования момента. Высокую плавность реостатного регулирования момента обеспечивают способы автоматического регулирования сопротивления Rдоб в целях поддержания момента. В качестве примера на рис.7.3 представлена функциональная схема релейного автоматического регулирования тока ротора и момента асинхронного двигателя.

Характеристика релейного элемента приведена на рис.7.3,б: переход от открытого состояния ключа к закрытому осуществляется при сигнале на входе uвх=U3, обратное переключение - при uвх=U0. Как показано на рисунке, эти переключения соответствуют значениям тока

Для анализа электромагнитных переходных процессов, протекающих в схеме, можно воспользоваться схемой замещения, приведенной к цепи выпрямленного тока ротора рис.7.4). Здесь в цепь выпрямленного тока введено сопротивление R'x, учитывающее снижение среднего выпрямленного напряжения, обусловленное коммутацией токов фаз:
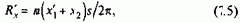
а также приведенные к цепи выпрямленного тока активные сопротивления двух фаз статора 2R'1s, ротора 2R2, сглаживающего реактора Rcp, а также его индуктивность Lcp. Сопротивление Rдоб в соответствии со схемой на рис.7.3 шунтировано тиристорным ключом ТК.

Если пренебречь временем переключения ключа, процессы изменения выпрямленного тока при переключениях сопротивления Rдоб описываются для открытого состояния ключа уравнением

а при закрытом ключе


эквивалентное сопротивление.
При принятом допущении начальный ток при закрытом состоянии ключа равен Iнач з, а при открытом Iнач о. Изменения тока определяются решениями (7.6) и (7.7):


где t1 - время, когда ido=Iначз;

Зависимость выпрямленного тока от времени, определяемая (7.8-7.11), для конкретного значения s и w представлена на рис.7.5,я. На участке 0<t<t1 ключ ТК открыт, и ток изменяется от начального значения, стремясь к установившемуся Ido, но через время t1 достигается значение id=Iначз, и ключ ТК закрывается. Период коммутации Тк можно определить, подставив в (7.8) значения id=Iконо=Iначз и t=t1, а в (7.9)- id=Iконз=Iначо и t=TK-t1.
 |

Решив полученные уравнения, и с их помощью получим
Из (7.12) следует, что частота коммутации тока fк=1/Тк является величиной переменной. При увеличении скорости и уменьшении скольжения s ток Idо уменьшается до значения Iнач 3, частота коммутации становится равной нулю, ключ ТК остается в открытом состоянии, и двигатель работает на естественной характеристике 1 (рис.7.5,б). При уменьшении скорости и возрастании s ток Id3 увеличивается до значения Iнач 0, возрастает до бесконечности время закрытого состояния ключа Tк-t1 и двигатель работает на реостатной характеристике 2.
При промежуточных значениях скорости и скольжения частота коммутаций велика, колебания тока при высоком коэффициенте возврата релейного элемента незначительны. Пренебрегая пульсациями тока, можно принять Id=Id.ср и определить выпрямленное напряжение:

потери в роторной цепи двигателя

а затем из условия
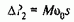
получить приближенную формулу для электромагнитного момента

При Uзт=Uзт1=const Idcp=Id cp1=const и М=М1=const (прямая 3 на рис.7.5,б). Задавая другие значения Uзт=const, можно получить ряд неизменных значений момента в пределах изменения скорости от характеристики 1 до характеристики 2 (Uзт2, Uзт3 соответствуют моменты М2, М3 и характеристики 4, 5).
Чем выше чувствительность релейного элемента, тем выше точность регулирования тока.Однако при этом возрастает максимальная частота fк=1/Tк. Известно, что возможная частота коммутации тиристорного (транзисторного) ключа ограничена, чем ограничивается и реальная точность релейного регулирования момента и тока двигателя.
Реостатное регулирование скорости

При оценке точности реостатного регулирования момента было установлено, что изменение скорости вследствие электромеханической связи является возмущением и тем более сильным, чем выше модуль жесткости характеристики. При регулировании скорости точность реостатного регулирования, напротив, повышается с увеличением модуля жесткости, а возмущением являются изменения нагрузки на валу двигателя. В этом можно убедиться, рассматривая рис.8.1. Введение добавочного резистора приводит к снижению средней скорости от wср.max на естественной характеристике 1 до wcp на реостатной характеристике 2, при этом, если Мc=Мсср=const, скорость электропривода поддерживается постоянной w=wср=const. Однако изменения статической нагрузки в пределах от Мсmaх до Мсmin вызывают абсолютную ошибку регулирования

где bи - модуль жесткости искусственной характеристики. Соответствующее значение относительной ошибки

Из (8.2) и (8.3) следует, что абсолютная и относительная ошибки регулирования по мере увеличения сопротивления Rдоб увеличиваются, причем особенно быстро увеличивается относительная ошибка, так как при увеличении Rдоб уменьшаются и bи и wсp.
Если в (8.3) принять

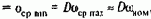

Соотношение (8.4) свидетельствует о том, что при реостатном регулировании при широких пределах изменения нагрузки возможный диапазон регулирования скорости невелик даже при невысокой требуемой точности регулирования. Практически при реостатном регулировании возможный диапазон регулирования скорости ограничивается значениями D=1,5¸2.
При использовании реостатного регулирования следует иметь в виду, что точность регулирования скорости может дополнительно снижаться вследствие колебания других факторов, например, колебание напряжения сети, температурные изменения сопротивлений обмоток и т.п.
Плавность реостатного регулирования скорости невелика, так как для переключения ступеней регулировочного резистора требуется предусматривать контакторы. При этом стремление уменьшить массогабаритные показатели и стоимость панели управления обычно вынуждает ограничивать число ступеней значениями 3-6. К числу достоинств реостатного регулирования относятся простота и невысокие затраты на реализацию. Однако не достатком этого способа является увеличение потерь энергии в силовой цепи по мере снижения скорости:
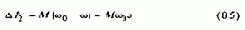
При номинальной нагрузке потери энергии тем больше, чем больше диапазон регулирования скорости:

Поэтому КПД электропривода при реостатном регулировании быстро снижается по мере расширения пределов регулирования скорости. Коэффициент мощности асинхронного электропривода при этом сохраняется на уровне номинального значения. Если предположить, что двигатель имеет независимую вентиляцию, в качестве критерия допустимой по нагреву нагрузки можно принять ток силовой цепи двигателя Iдв=Iном. В общем случае при реостатном регулировании для асинхронного двигателя

Аналогично и для двигателя постоянного тока с независимым или последовательным возбуждением получим
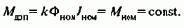

Таковы основные показатели реостатного регулирования скорости в разомкнутой системе. Точность и плавность этого способа регулирования скорости могут быть существенно увеличены в замкнутой системе автоматического регулирования скорости по отклонению.
Для осуществления автоматического реостатного регулирования скорости асинхронного двигателя может быть использована система релейного регулирования момента (см. рис.7.3), если ее дополнить отрицательной обратной связью по скорости по схеме, показанной на рис.8.2,а.
Уравнение механической характеристики электропривода в замкнутой системе регулирования можно записать на основе линеаризации зависимости (7.15)

положив Idз=Uзт/kот и приняв в качестве оценки инерционности контура релейного регулирования тока Tm значение постоянной времени Т0, соответствующей открытому состоянию тиристорного ключа ТК (см. §7.2). При этих условиях для схемы на рис.8.2,а можно записать

Отсюда

где
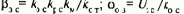
Положив в (8.9) р=0, получим уравнение статической механической характеристики в виде

Механические характеристики, соответствующие различным значениям U3C, показаны на рис.8.2,б. Пределы, в которых регулятор скорости может поддерживать скорость постоянной, ограничены при малых нагрузках реостатной характеристикой 1 (резистор Rдоб не выключается), а при больших - характеристикой 2, которая определяется максимальным значением выходного напряжения регулятора скорости, соответствующим насыщению его характеристики, показанной на рис.8.2,a. Объясняется это тем, что в данной схеме выходное напряжение PC является сигналом задания тока Uзт, а следовательно, и момента М.
Модуль жесткости статической характеристики bзс пропорционален koc, подбором значений которого можно получить достаточно жесткие регулировочные механические характеристики. Однако при этом следует иметь в виду, что введение обратной связи по скорости влияет на динамику системы.
С помощью (8.8) и уравнения движения электропривода на рис.8.3,a построена структурная схема рассматриваемого контура регулирования скорости. Для анализа процессов по управляющему воздействию положим в ней Мc=0 и приведем ее к единичной обратной связи. Структурная схема примет вид, показанный на рис.8.3,б. В схеме принято обозначение электромеханической постоянной времени в замкнутой системе:

Соответствующая ЛАЧХ разомкнутого контура представлена на рис.8.3,е. Как видно из рисунка, быстродействие контура регулирования ограничивается Тm=T0, так как для получения требуемого качества регулирования необходимо выполнение условия Tмз>Т0, а значения Тмз по мере увеличения kос уменьшаются в обратно пропорциональной зависимости.
Настройке на технический оптимум соответствует соотношение постоянных времени контура aс=Тмз/Тm=Тмз/Т0=2. Такое соотношение обеспечивается при следующем значении коэффициента обратной связи по скорости:
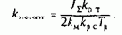
где Тm=Т0.

Для того чтобы качество регулирования оставалось высоким во всем диапазоне регулирования, расчетное значение постоянной времени Тm необходимо принимать равным наибольшему значению Т0.
Соотношение (8.12) характеризует предельную жесткость механической характеристики, которую можно получить в данной схеме при заданном качестве регулирования без применения динамической коррекции.
Режим динамического торможения асинхронного двигателя
Механическая характеристика на рис.3.42,а при f1=0 соответствует режиму динамического торможения асинхронного двигателя при его независимом возбуждении со стороны статора постоянным током I1. Такой режим возможен при питании от преобразователя частоты со свойствами источника тока при задании uзч=0 (f1=0). Однако в современном асинхронном электроприводе режим динамического торможения чаще используется для останова двигателя, получающего питание от сети, либо для регулирования скорости. Для осуществления режима динамического торможения асинхронный двигатель отключается от сети переменного тока и включается по схеме, приведенной на рис.3.44,а. При этом обмотка статора может быть соединена либо в звезду, либо в треугольник, в отдельных случаях подключают свободную фазу к одной из работающих, как показано на рис.3.44,a штриховой линией. Применяются и более сложные переключения обмоток статора для увеличения результирующей МДС при данном токе Iп или напряжении Uп.

Определение эквивалентного тока I1=Iэкв, исходя из этого условия, не представляет затруднений. В качестве примера на рис.3.44,б приведена наиболее употребительная схема при соединении обмоток в звезду, а на рис.3.44,в векторным суммированием МДС фаз обмоток определена результирующая МДС для этой схемы:
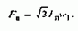
Эквивалентный ток определим, приравняв Fп амплитуде результирующей МДС, создаваемой трехфазным током I1=Iэкв:
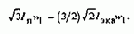
Следовательно, в данной схеме

Подставляя в полученные в §3.13 соотношения I1=Iэкв и w0=0, можно использовать их для анализа динамического торможения. Выражение абсолютного скольжения для режима динамического торможения имеет вид
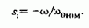
В соответствии с выражением критического момента Мк1 и критического скольжения sk1 в (3.109) для режима динамического торможения можно записать

Нетрудно видеть, что введение добавочных резисторов в цепь ротора при динамическом торможении снижает жесткость рабочего участка, так же, как и при двигательном режиме.
Режимы преобразования энергии и ограничения, накладываемые на их протекание
Режимы работы электромеханического преобразователя, возможные с точки зрения направления потоков энергии, представлены на рис.2.9.
Процессам преобразования электрической энергии в механическую, т. е. двигательному режиму преобразователя, соответствуют направления потоков мощности, показанные на рис.2.9,0. При этом поступающая из сети электрическая мощность Рс в основном преобразуется в механическую Pмех и частично теряется в виде теплоты в активных сопротивлениях и стали машины.
Электрическая машина обратима, поэтому, если подвести к ее валу механическую мощность Рмех, она может работать генератором электрической энергии параллельно с сетью, отдавая в сеть мощность - Рс. При этом часть поступающей в машину механической мощности также теряется в виде тепловых потерь DРТ (рис.2.9,б). Этот тормозной режим работы двигателя параллельно с сетью иногда называют режимом рекуперативного торможения.

Режим работы двигателя автономным генератором (не связанным с сетью) представлен схемой на рис.2.9,г. В этом режиме, называемом режимом динамического торможения, подводимая к валу механическая мощность преобразуется в электрическую и затем выделяется в виде теплоты в сопротивлениях силовых цепей и стали машины.
На рис.2.9,д показаны статические механические характеристики двигателя, соответствующие двум направлениям вращения его ротора. В первом и третьем квадрантах механическая мощность Pмех=М·w положительна - эти квадранты соответствуют двигательным режимам работы электромеханического преобразователя. Во втором и четвертом квадрантах мощность Рмех отрицательна, эти квадранты определяют область тормозных режимов работы преобразователя.
Процессы электромеханического преобразования энергии сопровождаются неизбежными потерями энергии в активных сопротивлениях обмоток машин, в стали магнитопроводов, а также механическими потерями.
Энергия потерь выделяется в виде теплоты в соответствующих элементах двигателя и вызывает его нагревание. Известно, что потери энергии в двигателе можно представить в виде суммы постоянных и переменных потерь. Постоянные потери DРС от момента, развиваемого двигателем и соответственно от токов, протекающих по его силовым обмоткам, практически не зависят. Переменные потери DPv представляют собой потери в активных сопротивлениях силовых цепей, которые пропорциональны квадрату тока I протекающего по этим сопротивлениям. Следовательно,

Увеличение количества полезной энергии, вырабатываемой двигателем в единицу времени, влечет за собой увеличение потребляемого из сети тока и соответствующее возрастание переменных и суммарных потерь. Поэтому при возрастании полезной нагрузки двигателя увеличивается количество теплоты, выделяемое в его массе в единицу времени, что вызывает повышение температуры его частей. Чем больше вырабатываемая двигателем полезная мощность, тем больше температура, до которой нагреваются его детали в процессе работы. Максимально допустимая температура двигателя ограничивается максимально допустимой температурой его элемента, наиболее чувствительного к превышению температуры. До настоящего времени таким элементом является изоляция обмоток, для которой допустимая температура ниже, чем для других частей машины, а превышение допустимой температуры вызывает резкое ускорение старения изоляции. Изложенные положения определяют важнейшее ограничение, накладываемое на процессы электромеханического преобразования энергии, - ограничение по нагреву двигателя. Полезная мощность, развиваемая двигателем, потребляемый из сети ток, электромагнитный момент двигателя не должны достигать значений, при которых рабочая температура двигателя может превысить допустимую. Допустимая по нагреву нагрузка двигателя называется его номинальной нагрузкой и указывается в паспортных и каталожных данных. Таким образом, номинальная нагрузка - это такая нагрузка двигателя, при которой двигатель, работая в номинальном режиме (продолжительном, повторно-кратковременном или др., см.
гл. 5), нагревается до допустимой температуры. К числу номинальных данных двигателя относятся номинальная мощность на валу Pном, номинальный ток Iном, номинальные напряжения питания обмоток Uном и частота fном, номинальная скорость wном (обычно указывается частота вращения n, об/мин). Для двигателей переменного тока в число номинальных данных включаются КПД hном и коэффициент мощности cos фном. Для двигателей постоянного тока номинальный КПД определяется:
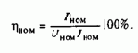
Вследствие тепловой инерции кратковременные перегрузки, например, в процессе пуска при достаточно малой продолжительности, не могут вызвать заметного изменения температуры частей двигателя. Поэтому ограничения, накладываемые нагревом, не исключают возможности кратковременного превышения номинальной нагрузки двигателя, допустимое значение которого определяется так называемой перегрузочной способностью двигателя:
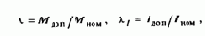
где Мдоп, Iдоп - максимально допустимый момент и ток двигателя при кратковременной перегрузке.
Перегрузочная способность двигателя ограничивается различными причинами. Для двигателей постоянного тока это ограничение является наиболее жестким, так как связано с условиями коммутации тока якоря коллектором. Известно, что перегрузка этой машины по току приводит к возрастанию искрения под щетками. При недопустимо большом токе искрение достигает опасных размеров, при которых возможно перекрытие коллектора дугой,- так называемый круговой огонь на коллекторе, который обычно выводит машину из строя. Наибольшее значение тока, при котором обеспечивается удовлетворительная коммутация, и ограничивает предельно допустимое значение момента двигателя Мдоп.
Условия коммутации тока на коллекторе машин постоянного тока накладывают дополнительное ограничение на режимы преобразования энергии в машинах постоянного тока. Искрение на коллекторе зависит не только от тока якоря, но и от скорости его изменения во времени, так как при быстрых изменениях тока имеет место отставание потока дополнительных полюсов от тока якоря вследствие электромагнитной инерции и наличия вихревых токов.Поэтому при работе машины постоянного тока должно выполняться условие diя/dt<(di/dt)доп, где (diя/dt)дon - максимально допустимая по условиям коммутации скорость изменения тока якоря. Соответственно должна быть ограничена и максимальная скорость изменения момента двигателя.
Для бесколлекторных машин переменного тока допустимы значительно большие перегрузки по току силовых цепей, чем для машин с коллекторами. При этом значения Мдоп обычно ограничиваются наибольшим моментом, который машина способна развить при номинальном напряжении сети и номинальном возбуждении, если таковое имеется. Обычно при оценке Мдоп следует учитывать допустимое по нормам снижение напряжения сети относительно его номинального значения.
овый режим работы синхронного электромеханического преобразователя
Важной особенностью синхронного двигателя является возможность фиксации положения его ротора путем подключения обмоток фаз статора к источнику постоянного напряжения. Для анализа этой возможности удобно использовать схему модели синхронного двигателя, приведенную на рис.3.46,б, приняв, что обмотка статора по оси а подключена к источнику напряжения U1п и в ней протекает постоянный ток I1a=I1п, а обмотка 1b отключена и i1b=0. Создаваемое обмоткой 1a поле статора направлено по оси a (w0эл=0, f0эл=0), и в результате взаимодействия с ним возбужденного ротора возникает синхронизирующий момент. Определим зависимость синхронизирующего момента от угла поворота ротора с помощью последнего уравнения системы (3.114):

Так как в осях a, b i1a=I1п; i1b=0, то преобразованные к осям d, q с помощью формул (2.15). Потокосцепления обмоток статора

токи статора имеют значения:
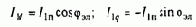
Подставив выражения токов и потокосцеплений в (3.125)


Примем, что Мс=0 и в статическом режиме ротор занимает положение, соответствующее фэл=0. Если в этом положении, как показано на рис.3.51, отключить обмотку 1a и включить на напряжение U1п обмотку 1b, результирующий вектор I1 скачком повернется на угол Dфш=90°, значение ф0эл изменится и станет равным Dфш, при этом возникнет синхронизирующий момент, определяемый кривой 2, который будет стремиться вновь совместить ось ротора с вектором поля статора и вызывать поворот ротора в сторону новой точки фиксации.
Зависимость М=f(фэл) для участка, где ф0эл=Dфш, показана на рис.3.51 (кривая 2). Кривая 2 определяется (3.126) при подстановке вместо фэл угла
f0эл-fэл=Dfш-fэл.
Рассматривая рис.3.51, можно видеть, что указанное переключение обмоток определяет поворот ротора на один шаг Dфш. Отключением обмотки 1b и включением обмотки 1a на напряжение –U1n вектор поля статора скачком поворачивается еще на один шаг, ротор занимает положение фэл=2Dфш и т. д. Таким путем можно задавать дискретные перемещения ротора двигателя, соответствующие определенному числу шагов. Средняя скорость перемещения при этом определится частотой импульсов тока, подаваемых в обмотки статора:
wcp=w0ср=Dfш/Dtш=f1Dfш (3.127)
 |
Кривая М=f(фэл) на рис.3.51 свидетельствует о том, что среднее по пройденному пути значение электромагнитного момента меньше, чем максимум момента по угловой характеристике, и зависит от угла, при котором осуществляется коммутация токов. Наибольшее значение среднего момента соответствует коммутации в точках пересечения кривых 1-8, обозначенных a1-а8, при этом средний за один шаг момент определяется соотношением
где m - число фаз двигателя.
Средний момент во времени может несколько отличаться от (3.128) в сторону уменьшения в связи с пульсациями скорости ротора. При f1=const статическая механическая характеристика в шаговом режиме при малых значениях f1 имеет вид, показанный на рис.3.52,а (1).

Проведенный анализ работы синхронного двигателя в шаговом режиме при питании обмоток статора от источника напряжения справедлив только для небольших частот коммутации токов.
При изменении частоты в широких пределах для строгого описания механической характеристики двигателя следует использовать систему уравнений (3.114) в записи для шагового режима:

Особенностью (3.129) является ступенчатый характер изменения ф0эл(t). Необходимость решения системы для каждого шага двигателя усложняет задачу, поэтому анализ динамики шагового режима обычно осуществляется с помощью ЭВМ. Он показывает, что при питании от источника напряжения с возрастанием частоты f1 увеличивается ЭДС статорных обмоток E1 и ток I1п снижается. Возрастающее влияние электромагнитной инерции приводит к изменению формы токов i1a и i1b, показанных на рис.3.51. Эти факторы определяют снижение момента Мсрmах, поэтому перегрузочная способность двигателя с ростом частоты уменьшается, как показано на рис.3.52,а.
В более широком диапазоне частот проведенный с помощью (3.126) анализ справедлив для шагового режима при питании всех обмоток двигателя от источников тока. В этом случае Iв=const, токи статора имеют форму, близкую к показанной на рис.3.51, и угловая характеристика определяется (3.126) при замене фэл на фоэл-фэл:

Семейство механических характеристик, соответствующих этим условиям, представлено на рис.3.52,б. Здесь перегрузочная способность двигателя в широком частотном диапазоне остается практически неизменной.
Таким образом, в шаговом режиме синхронный двигатель способен отрабатывать перемещения, задаваемые числом электрических импульсов, коммутирующих токи статора в требуемой последовательности. Жесткая связь между числом шагов перемещения ротора и числом электрических импульсов является замечательным свойством этого двигателя, широко используемым в практике дискретного электропривода с цифровым управлением. Для этих целей разработаны и выпускаются промышленностью серии специальных синхронных двигателей, называемых шаговыми электродвигателями.
Шаговые электродвигатели имеют небольшую (до 4 кВт) мощность и исполняются с различным числом фаз (m=3, 4, 5...) и числом пар полюсов рп> 2.
От этих параметров зависит значение шага:

Значение шага определяет точность отработки перемещений при показанном на рис.3.51 способе коммутации токов. На практике используются более сложные законы дискретного управления токами фаз статора, которые позволяют получать ряд промежуточных положений вектора /,, т. е. дробить шаг (3 125) на более мелкие дискреты и увеличивать точность управления движением электропривода.
Конструктивно шаговые двигатели имеют ряд исполнений по способу возбуждения (возбуждение ротора постоянным током, возбуждение с помощью постоянных магнитов, реактивные двигатели с Iв=0) и по характеру движения (двигатели с вращательным движением ротора, двигатели с линейным движением ротора, двигатели с многокоординатным линейным движением ротора).
Схема модели синхронного двигателя на рис.3.46,б при соответствующем законе коммутации токов обмоток статора полностью соответствует реальным шаговым двигателям различного исполнения. Поэтому проведенный анализ шагового режима работы отражает особенности шаговых двигателей. В частности, показанные на рис.3.51 зависимости наиболее близко соответствуют шаговым двигателям с питанием обмоток статора от источников тока и постоянными магнитами на роторе при рассмотренном законе импульсного возбуждения статора (без дробления шага).
Схемы шунтирования якоря двигателя постоянного тока с независимым возбуждением

Потенциометрическая схема регулирования скорости двигателей с независимым возбуждением приведена на рис.8.4,а. При двигателе небольшой мощности потенциометр может быть выполнен в виде реостата с подвижным контактом, путем перемещения которого подведенное к двигателю напряжение можно изменять от 0 до Uя=Uном. Электромеханическая и механическая характеристики двигателя в этой схеме могут быть получены по аналогии с системой УП-Д, если рассматривать потенциометр как источник регулируемого напряжения с внутренней ЭДС, равной напряжению холостого хода:

и внутренним сопротивлением

Подставив (8.13) и (8.14) в (6.6), получим уравнения характеристик в потенциометрической схеме в следующем виде:


Из (8 16) следует, что при перемещении движка потенциометра скорость идеального холостого хода уменьшается пропорционально aш, а модуль жесткости статической характеристики

является переменной, зависящей от aш При aш=0 и aш=1 жесткость bш равна жесткости естественной характеристики двигателя р при питании его от бесконечно мощной сети. При промежуточных значениях aш модуль жесткости bm<b, причем его минимум может быть определен обычным путем. Продифференцировав знаменатель (8.17) по aш и приравняв производную нулю, нетрудно определить значение aш=0,5, при котором bш имеет минимум:

Полученный результат позволяет построить механические характеристики двигателя в потенциометрической схеме (рис.8.4,б).
Рассматривая (8.18), можно установить, что минимальная жесткость механической характеристики в потенциометрической схеме по модулю тем больше, чем меньше сопротивление потенциометра Rп, т.
Для маломощных двигателей с последовательным возбуждением применима потенциометрическая схема регулирования напряжения, приложенного к силовой цепи двигателя, аналогичная рассмотренной на рис.8.4,а. Механические характеристики в этой схеме подобны характеристикам двигателя с последовательным возбуждением при различных напряжениях, но с увеличенным и изменяющимся от характеристики к характеристике суммарным сопротивлением якорной цепи.
Более благоприятная форма регулировочных механических характеристик получается в схеме шунтирования якоря, представленной на рис.8.6,а. В этой схеме сопротивление шунтирует только обмотку якоря двигателя, а обмотка возбуждения включается последовательно в цепь добавочного сопротивления Rдоб.
Как следствие, по сравнению с потенциометрической схемой здесь кроме снижения подведенного к цепи якоря двигателя напряжения достигается также эффект увеличения тока возбуждения за счет тока, протекающего по Rш. Благодаря последнему ток возбуждения при идеальном холостом ходе Iя=0 не равен нулю:
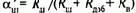
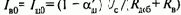
где
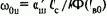 |
а скорость идеального холостого хода имеет ограниченное значение:
При w>w0ш двигатель переходит в генераторный режим, в котором поступающая с вала механическая энергия преобразуется в электрическую и теряется в виде теплоты в сопротивлениях Rя и Rш. Двигатель работает генератором параллельно с сетью на сопротивление Rш, и увеличение напряжения на Rш по мере роста скорости двигателя вызывает постепенное уменьшение потребляемого из сети тока, т. е. тока возбуждения. При IшRш®Uс Iв®0, а скорость двигателя неограниченно возрастает. Поэтому в области генераторного режима электромеханическая характеристика по мере роста скорости асимптотически приближается к прямой: Iя=IK2=-Uc/Rш Так как при этом поток стремится к нулю, момент двигателя в генераторном режиме вначале возрастает, достигает максимума и в дальнейшем при w®¥ М=kФIЯ®0, т.е. механическая характеристика асимптотически приближается к оси ординат слева.

е. чем больше его мощность.
Так как при регулировании поток двигателя остается постоянным (Ф=Фном), допустимая нагрузка двигателя без учета изменения условий охлаждения постоянна: М=Мном=const. При такой нагрузке двигателя мощность потенциометра превышает номинальную мощность двигателя, так как определяется напряжением сети Uном и наибольшим током потенциометра: Iпmax=Iном+Iпmax>Iном. Наибольший ток шунтирующей части потенциометра Iшmax быстро увеличивается при уменьшении Rп, поэтому минимальная жесткость механических характеристик в рассматриваемой схеме ограничивается приемлемой мощностью потенциометра. Тем самым ограничивается и возможный при данных пределах изменения нагрузки и требуемой точности диапазон регулирования скорости.
Плавность регулирования при небольшой мощности двигателя, позволяющей использовать ползунковый реостат, получается достаточно высокой. Однако с возрастанием мощности двигателя эта возможность исключается и регулирование осуществляется переключением ступеней регулировочных сопротивлений Rш и Rдоб с помощью силовой коммутирующей аппаратуры. При таком регулировании принимать суммарное сопротивление потенциометра Rп=Rш+Rдоб постоянным нецелесообразно, так как сопротивления Rш и Rдоб могут регулироваться независимо. Для этого случая (8.15) и (8.16) удобно представить в виде

Следует иметь в виду, как изменяются характеристики двигателя при изменении Rш при неизменном Rдоб или наоборот. Примем сначала Rдоб=const и будем изменять в (8.19) Rш(aш).
При изменении сопротивления шунтирующего резистора от бесконечности до нуля скорость идеального холостого хода непрерывно уменьшается от w0ном до 0, а жесткость возрастает от bш=с2/(Rя+Rдоб) до bш=b. Все эти характеристики пересекаются в одной точке, в которой ток якоря двигателя имеет значение

при скорости в режиме противовключения

Это можно установить, определив напряжение на выводах якоря двигателя при Iя=Iк1 и w=wк1:


При любом сопротивлении Rш ток Iш в этой точке равен нулю, поэтому она является общей для всего рассматриваемого семейства характеристик (рис 8 5,а)
Аналогичная общая точка обнаруживается и в семействе характеристик, соответствующем Rш=const и Rдо6=var (рис.8.5,б).
Все эти характеристики пересекаются в точке, где ток якоря определяется соотношением
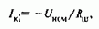
а скорость имеет значение

В этой точке напряжение на выводах двигателя равно напряжению сети, поэтому ток из сети не потребляется и значение Rд не сказывается на условиях работы двигателя. Графически точка IK1, wK1 определяется пересечением реостатной характеристики при RЯS=Rя+Rдоб(Rш=¥) и естественной характеристики динамического торможения (Rш=0) (прямые 1 и 2 на рис.8.5,a).
Точка Iк2 и wк2 определяется пересечением естественной характеристики двигателя 3 (Rдоб=0) и реостатной характеристики динамического торможения 4 (Rдоб=¥), как показано на рис.8.5,б.
Таким образом, механические характеристики в схеме шунтирования якоря двигателя с независимым возбуждением являются характеристиками двигателя, питаемого от источника регулируемого напряжения с относительно большим и изменяющимся при регулировании напряжения внутренним сопротивлением.
Благодаря ограниченной скорости идеального холостого хода эти характеристики создают более благоприятные условия для регулирования скорости, чем характеристики в потенциометрической схеме.

В схеме шунтирования якоря (см. рис.8.6,а) при определении допустимой нагрузки на регулировочных характеристиках необходимо учитывать, что в двигательном режиме Iв>Iя. Это вынуждает в качестве критерия допустимой нагрузки при постоянной теплоотдаче принимать номинальный ток обмотки возбуждения Iдоп=Iв.ном=Iном, что обеспечивает регулирование при потоке, равном номинальному, но требует по мере снижения скорости уменьшения момента Мдоп<Мном таким образом, чтобы выполнялось условие Iядоп=Iном-Iш.
В заключение отметим, что использование для регулирования напряжения резисторов является весьма простым и дешевым техническим решением, однако следует иметь в виду, что этот способ регулирования сопровождается значительными потерями в сопротивлениях Rш и Rдоб. Эти потери возрастают с уменьшением внутреннего сопротивления потенциометра и соответствующим увеличением получаемой жесткости характеристик. Поэтому по потерям энергии при регулировании потенциометрические схемы еще менее экономичны, чем реостатное регулирование.
Система генератор-двигатель
При рассмотрении свойств электромеханического преобразователя постоянного тока с независимым возбуждением было установлено, что наиболее широкие и благоприятные возможности управления процессами электромеханического преобразования энергии обеспечиваются изменением приложенного к якорной цепи двигателя напряжения uя. Для того чтобы зменять подведенное к якорю напряжение, используют различного вида управляемые преобразователи. До сравнительно недавнего времени для этой цели преимущественно применялись электромашинные преобразователи - генераторы постоянного тока, а основной системой регулируемого электропривода была система Г-Д. В настоящее время в связи с развитием вентильных преобразова телей ее применение сокращается, однако она продолжает
успешно применяться во многих ответственных промышленных установках.

Характеристики основных элементов системы Г-Д для наглядности показаны на том же рисунке в непосредственной близости от соответствующих элементов. Рассмотрим с их помощью особенности системы Г-Д как объекта управления.
В качестве приводных двигателей ПД применяются либо асинхронные, либо синхронные двигатели (на рис.6.4,а для случая использования синхронного двигателя штриховой линией показана цепь питания его обмотки возбуждения, ток которой Iвс, а напряжение питания Uвс).
Механическая характеристика 1 (рис.6.4,б) асинхронного двигателя AД обладает конечной статической жесткостью. Поэтому при изменении нагрузки на валу, создаваемой генератором Г при работе электропривода, скорость преобразовательного агрегата в небольших пределах изменяется (wг=var).
При использовании синхронного двигателя его скорость в статических режимах работы при разных нагрузках генератора остается неизменной (wг=const, прямая 2 на рис.6.4,б). Однако и в этом случае в динамических процессах скорость агрегата изменяется из-за ограниченной динамической жесткости механической характеристики синхронного двигателя bдин. В качестве примера на рис.6.4,б показана динамическая механическая характеристика 3 для случая установившихся колебаний нагрузки. Эта характеристика показывает, что и при синхронном двигателе в динамических процессах скорость агрегата может изменяться в небольших пределах относительно синхронной скорости двигателя (wг¹wг0).
Изменения скорости генератора приводят к изменению его ЭДС, следовательно влияют на работу электропривода. В частности, при асинхронном ПД с ростом нагрузки электропривода в двигательном режиме возрастает тормозной момент генератора и в соответствии с кривой 1 на рис.6.4,б скорость wг и ЭДС генератора Eг=k1Фгwг постепенно снижаются, что сказывается на скорости двигателя. В мощных электроприводах, для которых и применяется система Г-Д, это снижение составляет 1,5-2% и вызывает примерно такое же снижение скорости электропривода w в дополнение к другим факторам.
Преимуществами асинхронного приводного двигателя являются его меньшая колебательность, большая простота и надежность. Однако следует учитывать, что благодаря возбуждению постоянным током синхронный двигатель менее критичен к колебаниям напряжения сети, особенно при наличии системы автоматического регулирования тока возбуждения.
Номинальная мощность возбуждения мощных генераторов постоянного тока Pв.ном=Uв.ном·Iв.ном
достигает 0,5-1% номинальной мощности генератора, т.
е. составляет киловатты и десятки киловатт. Для осуществления автоматического регулирования коэффициент усиления системы Г-Д по мощности недостаточен, поэтому в цепь возбуждения генератора вводятся усилители мощности.
До недавнего времени для этой цели использовались электромашинные и позже магнитные усилители. Последние еще находят применение в ряде серийных электроприводов, выпускаемых в настоящее время. Однако основным видом возбудителей в современных системах Г-Д являются тиристорные и транзисторные преобразователи, обладающие весьма высоким быстродействием и коэффициентом усиления по мощности, составляющим сотни тысяч. Примерная характеристика тиристорного возбудителя Uв1=f(Uу) представлена на рис.6.4,в. При линейной зависимости угла регулирования от Uy ее рабочий участок составляет часть синусоиды, при арккосинусоидальной он линеен. При дальнейшем рассмотрении эта кривая и в первом случае линеаризуется без большой погрешности. С учетом небольшого запаздывания и малых постоянных времени фильтров (ТS=Гтв) динамические процессы тиристорного возбудителя ТВ при этом описываются уравнением
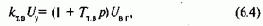
где kтв=UВ.Г./Uy - коэффициент усиления тиристорного возбудителя по напряжению.
Следует заметить, что основным видом тиристорного возбудителя в настоящее время является преобразователь с раздельным управлением, в характеристике которого в зоне прерывистых токов проявляется неоднозначность. Однако в связи с большой постоянной времени нагрузки это влияние незначительно и здесь не учтено.
Основной элемент энергетической части системы управления - генератор Г - также обладает нелинейной и неоднозначной характеристикой Eг=f(Uвг) при wг=const, которая представлена на рис.6.4,г кривой 1, линейной на основной части при ненасыщенной магнитной цепи. Вследствие гистерезиса в ней проявляется существенная неоднозначность (кривая 2). Учет гистерезиса усложняет анализ динамических процессов, так как каждым изменениям возбуждения соответствуют частные петли гистерезиса, лежащие внутри предельной петли 2, соответствующей циклам перемагничивания от +Eгном до ~Eгном и обратно.
Для выявления основных динамических свойств системы Г-Д гистерезисом можно пренебречь и для линейного участка характеристики 1 записать

где kг=Eг/Uвг при wг=const; Tг=Lвг/Rвг - постоянная времени генератора.
Уравнение механической характеристики электропривода, управляемого по системе Г-Д, получим с помощью уравнения электрического равновесия для якорной цепи машин:
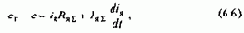
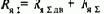

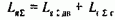

Уравнение (6.6) можно представить в виде

где с=k·Фном- коэффициент ЭДС двигателя; w0=ег/с - скорость идеального холостого хода в системе Г-Д; Тя=LяS/RяS.
Заменив в (6.7) iя на М=сiя, получим уравнение механической характеристики в системе Г-Д:

где bе=с2/RяS - модуль статической жесткости механической характеристики в системе Г-Д.
Сравнивая (6.8) с (3.41), можно установить их полную аналогию по форме. При принятых допущениях механические характеристики двигателя при питании от сети и от индивидуального генератора отличаются только значениями RяS и LЯS, если в качестве управляющего воздействия рассматривать не напряжение uя, а ЭДС генератора ег.
На рис.6.4,д представлена естественная механическая характеристика двигателя при питании от сети (прямая 1) и естественная характеристика в системе Г-Д (прямая 2). Так как генератор имеет примерно ту же мощность, что и двигатель, то RяSдв=RяSг. Соответственно модуль жесткости в системе Г-Д примерно в 2 раза меньше, чем модуль жесткости b при бесконечно мощной сети.
Характеристика 2 соответствует такой ЭДС генератора Ег=Егном, при которой двигатель работает в номинальном режиме при М=МНОМ, w=wном.
Это значение E1 больше, чем номинальное напряжение двигателя:

Как следствие, в разомкнутой системе Г-Д скорость идеального холостого хода w0ном=Eгном/с больше, чем w0=Uном/c при питании от сети.
Изменением ЭДС генератора Eг в системе Г-Д обеспечивается непрерывное плавное управление моментом и скоростью электропривода во всех четырех квадрантах координат механической характеристики при неизменной жесткости bе=const.
В качестве примера на рис.6.4, д показаны две искусственные характеристики 3 и 4, соответствующие значениям Е=Е'г=const и Е=-Ег"=const на рис.6.4,г.
С помощью уравнений (6.4)-(6.6) и уравнения движения электропривода при с12=¥ в виде
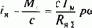

Опираясь на проведенный выше анализ, можно сделать вывод, что если изменять напряжение uу по закону, обеспечивающему линейное нарастание ЭДС генератора ег=bt, то в системе Г-Д w0=(b/c)t=e0t и зависимости момента М(t) и скорости w(t) будут иметь при прочих равных условиях тот же характер, что и на рис.4.30.
Отличием структуры системы Г-Д от рассмотренной выше структуры разомкнутой системы является наличие в цепи формирования управляющего воздействия двух инерционных звеньев с постоянными Tтв и Тг. Постоянная времени Гтв при полупроводниковой системе импульсно-фазового управления тири-сторным возбудителем весьма мала: Tтв=0,01 с Постоянная времени цепи возбуждения генератора Tг напротив, весьма велика: TГ=1¸3 с. Поэтому во многих случаях можно без заметной погрешности принять TТВ=0 и, обозначив k'г=kтвkг/с, представить структурную схему системы Г-Д, как показано на рис.6.5,б. Рассматривая эту схему, можно заключить, что при изменении управляющего воздействия иy скачком ЭДС генератора и скорость w0 в системе Г-Д изменяются по закону, определяемому переходной функцией инерционного звена с постоянной Тг:

Процессы в электромеханической системе с линейной механической характеристикой при изменении w0 по закону (6.10) были рассмотрены также в §4.9 и полностью характеризуют процессы в системе Г-Д при скачке управляющего воздействия.
Из (6.10) можно определить начальный темп нарастания управляющего воздействия

При данной Тг он определяется приложенным к обмотке возбуждения генератора напряжением Uвг=kтвUу и достигает наибольшего значения при UBmax=kTBUymax (см. рис.6.4,в).
Для получения требуемого времени нарастания ЭДС генератора до номинального значения tв необходимо форсировать процессы возбуждения путем повышения приложенного напряжения Требуемый коэффициент форсирования a=UBmax/UBHOM определяется из соотношения
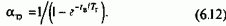


пропорциональна коэффициенту форсирования, реальное быстродействие в системе Г-Д ограничивается разумной степенью увеличения мощности возбудителя. При использовании электромашинных и магнитных возбудителей допустимые по этим соображениям значения amax<4. При возбуждении от полупроводниковых преобразователей в ряде случаев используют в 1,5-2 раза большие значения форсировок, что объясняется более высокими техническими показателями тиристорных и транзисторных возбудителей.
В заключение оценим экономичность системы Г-Д. Массогабаритные и энергетические показатели ее определяются необходимостью присущего этой системе трехкратного электромеханического преобразования энергии в трех входящих в систему электрических машинах: ПД, Г и Д. Как следствие, установленная мощность машин привода возрастает втрое, и благоприятные регулировочные возможности достигаются ценой существенных дополнительных затрат дефицитной меди, высококачественной стали и труда. Установка вращающегося преобразовательного агрегата требует сооружения специального фундамента, центровки агрегата, тщательной настройки коммутации тока коллектором генератора. Хотя регулирование путем изменения напряжения на якоре не вызывает дополнительных потерь в двигателе Д, преобразование энергии двигателем ПД и генератором Г сопровождается ее потерями и общий КПД системы Г-Д снижается:
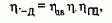
где hдв, hг, hпд - соответственно КПД электрических машин Д, Г и ПД.
Достоинствами системы Г-Д являются отсутствие искажений потребляемого из сети тока и относительно небольшое потребление реактивной мощности даже при асинхронном ПД. При применении синхронного двигателя в преобразовательном агрегате путем регулирования тока возбуждения можно обеспечить работу электропривода с cos ф=1 или с опережающим cos f для компенсации реактивной мощности, потребляемой другими установками.
В эксплуатации вращающийся преобразовательный агрегат, особенно его подшипники и коллектор генератора требуют внимания и ухода. При надлежащем уходе система Г-Д хорошо зарекомендовала себя в условиях эксплуатации.
Система источник тока – двигатель

При неизменном токе якоря момент двигателя пропорционален потоку:
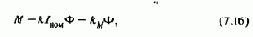
поэтому, изменяя поток двигателя, можно регулировать момент как по значению, так и по знаку. Питание двигателя от источника тока полностью исключает электромеханическую связь, так как любые изменения скорости и соответственно ЭДС двигателя компенсируются без запаздывания изменением ЭДС источника питания При этом ток нагрузки поддерживается неизменным. При Ф=const двигатель развивает постоянный момент при любых возмущениях, в том числе и при реальных пределах изменения скорости
Механические характеристики для различных значений потока двигателя в пределах от -ФНОМ до +ФНОМ показаны на рис.7.7.
Рассматривая их, можно установить, что электропривод по системе ИТ-Д обладает свойствами полностью управляемого источника момента, обеспечивающего при Ф=var точное и плавное регулирование момента в пределах от - Мном до +МНОМ как в двигательном, так и в тормозном режимах при любом направлении скорости.

Однако наиболее простые схемные решения с высокими показателями качества регулирования момента получаются при использовании параметрических источников тока, принцип действия которых основан на явлении резонанса в цепи переменного тока, содержащей индуктивные и емкостные элементы.
Известен ряд схем подобных преобразователей; наиболее распространенный вариант трехфазной схемы источника тока для питания двигателя постоянного тока показан на рис.7.8. Данная схема при определенном выборе параметров обеспечивает стабилизацию тока нагрузки в широких пределах изменения противо-ЭДС двигателя, ограничиваемых только линейностью и допустимым током и напряжением ее элементов, при этом благодаря симметрии схемы в установившихся режимах работы можно ограничиться рассмотрением работы одной фазы. Ток нагрузки одной фазы при принятых на схеме направлениях выразится так:

Токи реактивных элементов схемы определяются известными соотношениями:

Следовательно,
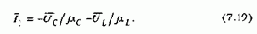
При хс=xl=х соотношение (7.19) принимает вид

где Uл=Uc+UL - линейное напряжение питающей сети.
Так как выпрямленный ток Id пропорционален эффективному значению тока I2, из (7.20) со всей очевидностью вытекает, что при идеальных линейных реактивных элементах ток якоря двигателя не зависит от противоЭДС двигателя и сопротивления цепи нагрузки и при Uл=const является постоянным: Iя=Id=kсхI2=const.
Индуктивно-емкостный преобразователь обладает высоким КПД и коэффициентом мощности, близким к единице. Однако наличие неуправляемого выпрямителя исключает возможность рекуперации энергии в сеть при тормозных режимах работы двигателя, что снижает управляемость привода. Зона поддержания момента постоянным при этом ограничивается областью двигательного режима и областью тормозного режима противовключе-ния, заключенной между осью абсцисс и характеристикой динамического торможения двигателя, соответствующей данному значению потока Ф и расширяющейся по мере ослабления поля.
Граничное значение скорости, при котором реверсивный источник тока переходит в режим рекуперации энергии, определяется соотношением


Из (7.21) следует, что ограничение пределов, в которых момент поддерживается постоянным, в рассмотренной схеме можно практически устранить введением в цепь якоря постоянно включенного или вводимого на время торможения дополнительного резистора Rя доб.
Система преобразователь частоты - асинхронный двигатель
Наиболее простым, дешевым и надежным электрическим двигателем является асинхронный короткозамкнутый двигатель, поэтому его использование в регулируемом электроприводе представляет особый интерес. Как было установлено, возможности регулирования, аналогичные возможностям изменения напряжения на якоре двигателя постоянного тока с независимым возбуждением, в асинхронном электроприводе обеспечиваются путем изменения частоты напряжения и тока статорной обмотки. Для реализации этих возможностей необходимо осуществлять питание статорной обмотки двигателя от управляемого преобразователя частоты.
Регулирование частоты представляет собой технически более сложную задачу, чем регулирование выпрямленного напряжения, так как, как правило, требует дополнительных ступеней преобразования энергии.

На рис.6.12 приведена схема вентильно-электромашинного преобразователя частоты, в котором регулирование скорости синхронного генератора производится по системе ТП-Д. Здесь вместо электромашинного агрегата, вырабатывающего регулируемое напряжение постоянного тока, применен более экономичный тиристорный преобразователь. Однако и в этом случае преобразователь частоты содержит три ступени преобразования энергии, из них две - электромеханического преобразования.
Схема непосредственного регулирования скорости по системе ТП-Д проще и дешевле, поэтому применение системы ПЧ-АД, показанной на рис.6.12, может иметь место только в специальных установках, например в случаях, когда двигатель постоянного тока не может быть применен для привода исполнительного механизма по техническим условиям.
В §3.11 было отмечено, что при изменении частоты необходимо регулировать напряжение или ток статорной обмотки асинхронного двигателя. В схеме на рис.6.12 соответственно присутствуют два канала управления: канал управления частотой (Uyч), воздействующий на скорость синхронного генератора СГ, и канал управления напряжением, воздействующий на возбуждение СГ(Uун).
Канал регулирования частоты имеет структуру системы ТП-Д (рис.6.12) и обладает значительной инерционностью, обусловленной механической инерцией преобразовательного агрегата ПД-СГ. Канал регулирования напряжения также инерционен в связи с наличием электромагнитной инерции цепи возбуждения синхронного генератора. Поэтому как объект управления представленная на рис.6.12 система обладает неблагоприятными свойствами.
Наименьшим числом ступеней преобразования энергии обладают вентильные преобразователи частоты Они содержат ступень преобразования переменного тока в постоянный и ступень инвертирования. Эти две ступени в самостоятельном виде присутствуют в преобразователях частоты со звеном постоянного тока В преобразователе частоты с непосредственной связью функции выпрямления и инвертирования совмещены в реверсивном преобразователе постоянного тока, выпрямленное напряжение или ток которого изменяются с требуемой частотой с помощью системы управления преобразователем. Как следствие, наиболее близкими к системе ТП-Д массогабаритными показателями обладает система ПЧ-АД с преобразователем с непосредственной связью, а система с преобразователями, содержащими ступень постоянного тока, уступает по этим показателям системе ТП-Д. Однако различия по мере совершенствования вентильных преобразователей частоты постепенно сокращаются, и существенные преимущества асинхронного двигателя определяют несомненную перспективность системы ПЧ-АД.

Канал управления частотой может осуществлять либо дискретное, либо непрерывное формирование частоты напряжения и тока. При непрерывном формировании синусоидальных напряжений или токов заданной частоты его можно считать практически безынерционным. Канал управления напряжением или током воздействует на тиристорный преобразователь, и его быстродействие может оцениваться быстродействием этого управляемого преобразователя

Как было установлено в §3.12, при таком управлении напряжением в схеме рис.6.13,а или током в схеме рис.6.13,5, которое обеспечивает постоянство потокосцепления Y1=const, или при постоянстве Ym или Y2 в пределах значений абсолютного скольжения sa£sk уравнение механической характеристики двигателя имеет вид
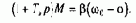
В системе ПЧ-АД (рис 6.13)
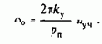
Дополнив эти уравнения уравнением движения электропривода, получим систему уравнений, которой соответствует представленная на рис.6.14 структурная схема системы ПЧ-АД.
Параметры b и Тэ в этой структуре должны соответствовать требуемому режиму работы электромеханического преобразователя: Y1=const, Ym=const или Y2=const.
Динамические свойства системы ПЧ-АД как объекта управления менее благоприятны, чем динамические свойства регулируемых электроприводов постоянного тока, в связи с отсутствием независимого канала регулирования потока, аналогичного обмотке возбуждения двигателя с независимым возбуждением. Так, при питании от источника напряжения потокосцепления Y1, Y2, Ym сложно зависят от напряжения U1 частоты f1 и абсолютного скольжения sa.
Для поддержания потока на заданном уровне при этих условиях необходимо регулирование его либо по отклонению, либо по принципу компенсации.
В последнем случае управление напряжением uун (рис.6 13,о) или током uут (рис 6 13,б) реализуется на основе известной взаимосвязи между Y1, Ym, Y2 управляющими воздействиями U1 или I1 и факторами f1 и sa.
Взаимосвязь U1 и Y1 можно определить с помощью уравнений электрического равновесия, записанных в векторной форме для статического режима в осях х, у, и представить в виде


Зависимость (6.17а) позволяет для текущих значений частоты и абсолютного скольжения определять значения напряжения U1 которые в статическом режиме работы соответствуют условию

В динамических режимах изменениям момента двигателя соответствуют изменения угла между вектором напряжения







Для определения необходимых для такого управления количественных связей запишем уравнения механической характеристики в осях х, у (wк=w0эл):


Уравнения потокосцепления ротора

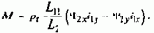
Поставив цель поддерживать постоянным вектор потокосцепления ротора


Подставляя эти соотношения и значения dY2x/dt=dY2y/dt=0 в уравнения механической характеристики, получаем
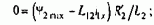

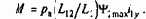
Отсюда

Векторная диаграмма, соответствующая полученным соотношениям, приведена на рис.6.13,в. Она показывает, что составляющая i1x вектора тока статора является намагничивающим током и при Y2=const, i1x=const. Составляющая i1y представляет собой активный ток, которому при Y2=const пропорционален момент двигателя. С помощью векторной диаграммы определим искомые соотношения, позволяющие обеспечить условие Y2=const в динамических процессах:

Следовательно, при частотно-токовом управлении электроприводом система управления преобразователем должна обеспечивать возможность формирования первой гармоники тока статора для поддержания Y2=const в соответствии с (6.176) и (6.17в):
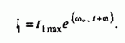
Поэтому показанный на рис.6.13,б инвертор тока ПЧ(ИТ) снабжен кроме входов управления амплитудой uут и частотой тока uуч также входом управления фазой тока ыуф. Уравнение механической характеристики при Y2=const

где
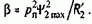
При идеальном поддержании Y2=const электромагнитная постоянная Тэ в структуре на рис.6.14 равна нулю. Однако практически в связи с неточностями компенсации возможные проявления электромагнитной инерции следует учитывать малой некомпенсируемой постоянной Тэ.
Значение Т3 при Y1=const определяется по (3.89). Этим же соотношением можно пользоваться при Ym=const, подставляя вместо хк значение х'2.
Однако следует отметить, что внимания заслуживают и такие законы управления, которые обеспечивают снижение потерь энергии, выделяющихся в двигателе. В частности, управление, близкое к оптимальному по критерию минимума потерь, осуществляется при поддержании абсолютного скольжения, равного критическому при всех нагрузках: sa=sk=const. Этому условию при каждом моменте М соответствуют наименьшие значения тока статора I1=I1min при М=const.
При использовании такого управления следует учитывать, что при уменьшении нагрузки от Мном до 0 снижение потерь достигается из-за уменьшения тока намагничивания Im, т.
е. потока машины Фm. А это означает, что при управлении при sa=sk=const основной поток изменяется в широких пределах, что приводит к сильному влиянию электромагнитной инерции, существенно снижающему быстродействие при регулировании координат.
Коэффициент полезного действия системы ПЧ-АД с вентильным преобразователем несколько ниже, чем в системе ТП-Д, если имеется звено постоянного тока, так как при этом преобразование напряжения и тока осуществляется дважды.
Однако и в этом случае в связи с малыми потерями энергии в тиристорах он остается достаточно высоким.
Коэффициент мощности в этой системе близок к значению коэффициента мощности в системе ТП-Д, если в качестве звена постоянного тока используется тиристорный преобразователь. Он достаточно высок только в системах с неуправляемым выпрямителем, однако при этом отсутствует возможность рекуперации энергии в сеть в тормозных режимах электропривода. Использование режимов рекуперации энергии может существенно снижать потребление энергии установкой за цикл работы, поэтому при сравнении вариантов системы этот фактор необходимо учитывать.
Система тиристорный преобразователь-двигатель
В силу отмеченных выше недостатков электромашинного преобразовательного агрегата на всех этапах развития электропривода много внимания уделялось поиску возможностей замены электромашинных преобразователей статическими вентильными преобразователями. В свое время получила некоторое распространение система управляемый ртутный выпрямитель - двигатель (УРВ-Д). Однако особенности ртутных вентилей - значительное падение напряжения в дуге, большие габариты, сложность эксплуатации, значительная мощность и несовершенство системы сеточного управления - не позволили этой системе успешно конкурировать с системой Г-Д Эта задача получила успешное решение только после создания полупроводниковых кремниевых вентилей и совершенных систем импульсно-фазово-го (СИФУ) управления на базе микроэлектроники, которые позволили разработать тиристорные преобразователи с высокими техническими показателями.
Схема системы ТП-Д представлена на рис.6.10,а. Двигатель постоянного тока Д получает питание от тиристорного преобразователя ТП, который преобразует напряжение сети переменного тока Uc в выпрямленное напряжение Uя, приложенное к цепи якоря двигателя. Для сглаживания пульсаций тока в цепь якоря введен сглаживающий реактор Р. Выпрямленное напряжение Uя зависит от угла регулирования а, противоЭДС нагрузки, тока нагрузки, падений напряжения на элементах силовой цепи преобразователя, и внешние характеристики преобразователя UTП=UЯ=f(Iя, Е) при a=const имеют сложный нелинейный вид.
Внешняя характеристика тиристорного преобразователя близка к линейной только при непрерывном токе нагрузки. При этом процессы в цепи выпрямленного тока определяются средними значениями напряжения и тока, что позволяет без большой погрешности представить преобразователь в качестве источника питания с ЭДС Еп и эквивалентным внутренним сопротивлением Rп экв. Значения Еп в этом режиме однозначно определяются утлом регулирования а и при линейной характеристике СИФУ зависимость а показана En=f(U) на рис.6.10,б (кривая 1) При замене реальной характеристики линеаризованной как динамическое звено системы электропривода тиристорный преобразователь в режиме непрерывного тока описывается уравнением
Наиболее существенные особенности в систему ТП- Д вносит использование нереверсивного тиристорного преобразователя. При этом система является неполноуправляемой, ток якоря может протекать только в одном направлении. Соответственно механические характеристики во втором и третьем квадрантах не существуют.
Учет особенностей, вносимых различными тиристорными преобразователями, при проектировании электропривода имеет важное практическое значение Ему уделяется главное внимание в курсе «Системы управления электропривода» при изучении свойств и методов построения и расчета различных систем ТП-Д. В данном курсе для выявления общих закономерностей регулируемого электропривода предполагается работа системы ТП-Д при непрерывном токе и используются уравнения (6.14)-(6.16).
Структурные схемы системы ТП-Д, соответствующие этим уравнениям и уравнению движения электропривода при жестких механических связях, представлены на рис.6.11,а и б. При составлении схемы на рис.6.11,б уравнение (6.14) представлено в виде
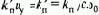
где
Система ТП-Д отличается весьма высоким быстродействием преобразователя. Постоянная времени Тп при полупроводниковой СИФУ не превосходит 0,01 с. Соответственно возможности создания быстродействующих электроприводов при переходе к системе ТП-Д существенно расширяются.
Оценим экономичность системы ТП-Д в сравнении с системой Г-Д. При использовании нереверсивного преобразователя установленная мощность системы ТП-Д составляет 2Рдв, т.е. меньше, чем для системы Г-Д. Однако при этом система ТП-Д имеет ограниченные технические возможности. В сравнимом варианте использования реверсивного преобразователя установленные мощности систем ТП-Д и Г-Д примерно одинаковы. Однако преимущества статического преобразователя перед вращающимся при этом говорят в пользу системы ТПД.
Важным достоинством системы ТП-Д является ее высокий КПД. Потери энергии в тиристорах при протекании номинального тока составляют 1-2% номинальной мощности привода. Поэтому даже с учетом потерь в реакторе и трансформаторе КПД преобразователя при мощности, составляющей десятки киловатт, достаточно высок.

Способы регулирования скорости асинхронного электропривода
Общие свойства регулируемого по скорости электропривода, рассмотренные ранее на основе обобщенной структуры электропривода с линеаризованной механической характеристикой, необходимо дополнить рассмотрением ряда частных возможностей регулирования скорости асинхронного электропривода, связанных с его особенностями Возможные способы регулирования скорости асинхронного электропривода можно разделить на три группы:
1) способы регулирования, при которых скольжение изменяется в широких пределах и потери, выделяющиеся в виде теплоты в элеменmax роторной цепи, пропорциональны скольжению;
2) способы, при которых абсолютное скольжение двигателя при регулировании остается небольшим и не достигает критического скольжения на естественной характеристике (sa<ske);
3) способы, при которых абсолютное скольжение при регулировании изменяется в широких пределах, но потери энергии скольжения в роторной цепи двигателя ограничены.
К первой группе способов регулирования скорости асинхронного электропривода относятся рассмотренное ранее реостатное регулирование, регулирование изменением напряжения на статоре двигателя, наложение механических характеристик в двухдви-гательном электроприводе, регулирование с помощью асинхронной муфты скольжения и др.
Изменение напряжения, рассмотренное в гл.7 как средство регулирования момента в разомкнутой системе может быть использовано для регулирования скорости в системе автоматического регулирования по отклонению. Для этого схемы с магнитным усилителем или тиристорным регулятором напряжения необходимо дополнить отрицательной связью по скорости Рассмотрим основные показатели такого способа регулирования.
Схема регулирования скорости асинхронного электропривода путем изменения напряжения на статоре приведена на рис 8 31 Здесь магнитный или тиристорный регулятор напряжения обозначен РН, введен регулятор скорости PC, выходное напряжение которого uy
воздействует на обмотку управления магнитного усилителя или на вход тиристорного регулятора напряжения На вход PC поданы сигнал задания uз.с и сигнал обратной связи по скорости uос, получаемый с якоря тахогенератора ТГ В цепь управления РН введен сигнал смещения, с помощью которого при uy=0 устанавливается минимальное напряжение на выходе РН.
Практически в схемах с магнитными усилителями для этой цели предусматривается отдельная обмотка смещения, а в тиристорных регуляторах напряжения для установки начального угла регулирования a0 обычно имеются соответствующие подстроечные элементы. При оценке условий регулирования скорости в системе тиристорный регулятор - асинхронный двигатель (ТРН-АД) необходимо учитывать, что напряжение на выходе тиристорного регулятора несинусоидально, зависит от утла регулирования а и от угла активно-индуктивной нагрузки fн, которой является асинхронный двигатель для ТРН при определенном скольжении s. Электромагнитный момент двигателя определяется первой гармоникой напряжения, а влияние высших гармоник невелико, и им можно пренебречь Поэтому для расчета механических характеристик двигателя необходимо знать зависимость первой гармоники напряжения U1 от напряжения управления Uy
при различных скольжениях s и соответственно различных фн.
Примерные зависимости U1/U1HOM от Uу/Yуном для ряда значений фн приведены на рис.8.32, причем в качестве UyHOM принято напряжение, которое обеспечивает изменение угла a от 0 до 150° при линейной характеристике a=f(Uу), а кривые построены при напряжении смещения Uсм, которое обеспечивает начальный угол a0=135°. Эти характеристики существенно нелинейны и неоднозначны в связи со значительной зависимостью напряжения от угла нагрузки фн.
Зависимость угла нагрузки fн от скольжения можно получить, воспользовавшись упрощенной схемой замещения двигателя, приведенной на рис.3.27,б:

где хэкв, Rэкв - эквивалентные активное и индуктивное сопротивления двигателя, определяемые относительно U1 по схеме замещения; R1S - суммарное активное сопротивление цепи статора, включая сопротивление фазы ТРH.
Анализ (8.88) показывает, что угол fн изменяется в функции скольжения быстро лишь при s<sk, а при sk< s<1 его изменения лежат в пределах 40-60°. Для этой области кривую U1=f(Uy) можно линеаризовать, как показано на рис.8.32 (прямая 1) и приближенно записать

где

Так как момент асинхронного двигателя пропорционален квадрату напряжения, можно записать

где Me(s) - момент при данном скольжении, определяемый по естественной механической характеристике двигателя; U1*==U1/UHOM - относительное значение первой гармоники напряжения питания двигателя.
При работе Uзс=const скорость двигателя в рабочей зоне механической характеристики поддерживается системой регулирования примерно постоянной, поэтому для режимов малых отклонений от точки статического равновесия (8.90) можно линеаризовать:




Подставив (8.91) в (8.89), получим уравнение механической характеристики для рассматриваемого режима:

где:

Таким образом, при принятых допущениях в замкнутой системе формируется линейная механическая характеристика со скоростью идеального холостого хода w0зс и модулем жесткости b3с, которые определяются заданием и коэффициентом обратной связи по скорости koc. При больших kос жесткость искусственных характеристик получается значительной, и уравнение (8.92) удовлетворительно описывает реальную механическую характеристику. Как показано на рис.8.33, отличия проявляются лишь в режиме, близком к холостому ходу, и при значениях напряжения, близких к U1ном. Иными словами, (8.92) удовлетворительно описывает механическую характеристику замкнутой системы электропривода в возможных пределах регулирования момента, рассмотренных в §7.7.
При данном способе регулирования потери в роторной цепи пропорциональны скольжению. Поэтому допустимый момент при регулировании скорости при независимой вентиляции двигателя можно определить из соотношения
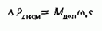
Откуда

Следовательно, для того чтобы при продолжительной работе с малой скоростью двигатель не нагревался сверх допустимой температуры, необходимо снижать его нагрузку в обратно пропорциональной зависимости от скольжения. Для двигателей с самовентиляцией это снижение должно быть больше с учетом ухудшения условий охлаждения по мере роста скольжения. Зависимость Мдоп=f(w) показана на рис.8.33.
Этот недостаток ограничивает область применения замкнутых систем асинхронного электропривода, основанных на регулировании напряжения, механизмами, у которых момент нагрузки при регулировании скорости быстро уменьшается, например механизмами с вентиляторной нагрузкой (см.§1.3).
Кроме того, этот способ успешно применяется в тех случаях, когда в рабочем цикле требуется кратковременное снижение скорости, а основное время электропривод работает на естественной характеристике.
Дополнительные возможности регулирования скорости дает применение многодвигательного электропривода. Рассмотрим эти возможности на примере двухдвигательного асинхронного электропривода, схема которого приведена на рис.8.34,а.
Благодаря наличию механической связи между роторами двигателей 1Д и 2Д в статических режимах работы угловые скорости двигателей одинаковы, а результирующий момент электропривода равен сумме моментов двигателей. При линеаризации механических характеристик результирующая механическая характеристика может быть получена в виде (4.127):

Рассматривая (8.94), можно убедиться, что путем целенаправленного изменения жесткостей механических характеристик двигателей, а также соотношения скоростей идеального холостого хода в двухдвигательном электроприводе можно получить результирующие искусственные характеристики, обеспечивающие регулирование скорости.

Наличие фазного ротора у каждого двигателя позволяет вводить в цепи ротора добавочные резисторы и таким образом изменять значения b1 и b2, а переключение двигателя 1Д в режим динамического торможения дает w01=0. При этом подбором жесткостей можно получить глубокое регулирование скорости, как показано на рис.8.34,б. Здесь добавочное сопротивление в цепи двигателя 1Д, работающего в режиме динамического торможения, равно нулю и жесткость характеристики 1 b1 максимальна. Для ограничения тока и увеличения жесткости результирующей характеристики в цепь ротора двигателя 2Д введен добавочный резистор со значительным сопротивлением (характеристика 2, sK2> sKe).
Жесткость рабочего участка результирующей характеристики 3 bрез=b1+b2, т. е. выше, чем жесткость b1 при Rдоб=0, а скорость идеального холостого хода w0и достаточно мала. При моменте нагрузки Мс результирующая механическая характеристика 3 обеспечивает устойчивую пониженную скорость wс.п.
Недостатком данного способа регулирования скорости являются значительные потери. Результирующий момент

т. е. двигатель 1Д для получения малой скорости, работая в режиме динамического торможения, подгружает двигатель 2Д моментом М1п, соответственно
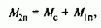
где М1п - тормозной момент 1Д при работе на пониженной скорости wс.п.
Как следствие, потери энергии в роторной части двигателя 2Д существенно больше, чем при реостатном регулировании (М2п>Mc).
Для того чтобы оценить допустимую нагрузку двухдвигатель-ного электропривода при пониженной скорости, необходимо для сравнения рассмотреть режим работы с полной скоростью, при котором оба двигателя подключены к сети переменного тока и работают на общий вал. Как показывает рис.8.34,в, в этом случае оба двигателя работают в двигательном режиме:
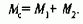
Сравнивая рис.8.34,б и в, можно заключить, что допустимый на низкой скорости момент Мдоп существенно меньше половины номинального момента агрегата Мдоп=М2ном-М1п.
Таким образом, если необходимо регулировать скорость при Мс=const, то при работе на полной скорости агрегат должен недоиспользоваться в 2,5-3 раза по мощности. Если на пониженной скорости электропривод должен работать малую долю времени цикла, то недоиспользование мощности агрегата из-за кратковременной перегрузки двигателя 2Д на малой скорости может быть сокращено до 1,25-1,5 раза. Поэтому наиболее целесообразно применение этого способа в случаях, когда работа с пониженной скоростью в цикле весьма кратковременна. При этом перегрузки на пониженной скорости не сказываются существенно на нагреве двигателей, а низкий КПД системы не может заметно ухудшить энергетические показатели электропривода.
При полной идентичности механических характеристик обоих двигателей каждый из них несет половину общей нагрузки, и при этих условиях номинальный момент агрегата равен:
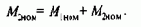
Однако практически, как показано на рис.8.34,в, естественные характеристики двигателей вследствие разброса параметров могут несколько различаться (b1е¹b2е). При этом моменты, развиваемые двигателями при w1=w2=wс, оказываются не равными:

На рис.8.34,в b2е>b1е, соответственно М2>M1. Так как по условиям нагрева двигателя должно быть М2=М2ном, пеpвый двигатель недогружается тем в большей степени, чем меньше жесткость его характеристики. Очевидно, что если при проектировании не учесть возможного несовпадения характеристик двигателей и выбрать двигатели из условия М1ном=М2ном=Мс ном/2, то двигатель с большей жесткостью bе примет на себя нагрузку, большую номинальной, и выйдет из строя.
Ко второй группе способов регулирования скорости асинхронного электропривода относятся частотное регулирование, особенности которого будут ниже рассмотрены, и регулирование путем изменения числа пар полюсов.
Регулирование скорости путем изменения числа пар полюсов осуществляется при питании двигателя от сети при f1=f1ном=const путем переключения одной статорной обмотки с треугольника на двойную звезду (рис.8.35,a) или со звезды на двойную звезду (рис.8.35,б). Число пар полюсов рп при этом изменяется вдвое, что вызывает соответствующие изменения скорости поля w0:
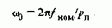

У двигателя с фазным ротором роторная обмотка выведена на контактные кольца, что создает возможность подвода напряжения не только к цепи статора, но и к цепи ротора. Активная цепь роторной обмотки, содержащая регулируемые источники напряжения, позволяет полезно использовать энергию скольжения и вследствие этого осуществлять экономичное регулирование скорости при широких пределах изменения скольжения двигателя. Этот характерный для асинхронного электропривода способ регулирования скорости подробно рассматривается ниже.
Стандартные настройки регулируемого электропривода
При последовательной коррекции структурная схема контура регулирования переменной х может быть представлена, как показано на рис.6.16, состоящей из регулятора с передаточной функцией Wp x и объекта регулирования с передаточной функцией Wopx. Передаточная функция разомкнутого контура

Примем, что передаточная функция объекта регулирования имеет вид

где tп - постоянное запаздывание; Ti - постоянные времени элементов объекта регулирования, расположенные в порядке убывания по значению.
Предположим, что передаточная функция регулятора реализована в виде

где l - число больших и средних постоянных времени. Тогда передаточная функция разомкнутого контура

Полученное выражение свидетельствует о том, что формированием передаточной функции регулятора можно направленно видоизменять передаточную функцию разомкнутого контура. Действительно, при k1=k'1, k2=k'2,..., kn=k'n и Tj=Ti исходная передаточная функция существенно видоизменяется:

В ней введением регулятора с передаточной функцией (6.26) и подбором его параметров исключено l инерционных звеньев, обладающих большими и средними Ti, сокращено п частных коэффициентов и введено интегрирующее звено.
Исключение из передаточной функции разомкнутого контура звеньев с большими и средними постоянными времени открывает возможности повышения быстродействия контура регулирования. Эта операция реальные физические инерционные звенья из контура, разумеется, не исключает Однако их действие, замедляющее протекание переходных процессов, компенсируется действием соответствующих форсирующих звеньев, содержащихся в регуляторе, ускоряющих в требуемой степени реакцию системы.

Пытаться компенсировать весьма малые постоянные времени звеньев контура нецелесообразно, так как технические трудности компенсации быстро возрастают при уменьшении значений постоянных времени, а влияние на быстродействие привода соответственно убывает. Особые трудности представляет компенсация дискретности и малого запаздывания tп ряда быстродействующих преобразователей. Как следствие, в (6.28) остались некомпенсированными несколько (m-l) малых постоянных Ti и постоянная tп. Достоинством (6.28) является возможность выбора требуемого значения постоянной Т0. Этот выбор и определяет настройку контура регулирования. Если выбрать Т0 из условия T0>Ti+1 где Ti+1, как было принято, является наибольшей из оставшихся некомпенсированными постоянных Ti, то можно представить частотные характеристики (6.28), как показано на рис.6.18 Низко- и среднечастотная асимптота ЛАЧХ имеет наклон -20 дБ/дек (прямая 1), а запас по фазе на частоте среза DY(Wc), определяемый по кривой 2, зависит от степени удаленности частоты среза 1/T0 от ближайшей частоты сопряжения 1/Тi+1. С учетом постоянной запаздывания tп, влияние которой в кривой 2 проявляется, запас по фазе на частоте среза составит:

Углы DY(Wc) в (6.29) невелики, так как на соответствующих частотах сопряжения arctgTiWi=arctg 1=p/4. Так как Т0>Тi+1, arctg TiWc<p/4 и приближенно можно принять arctgTiQC»ТiWс.
Следовательно,

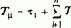
где - суммарная некомпенсированная постоянная контура регулирования, эквивалентная по потере запаса по фазе на частоте среза всем его реальным некомпенсированным инерционностям.
С учетом (6.30) передаточную функцию (6.28) можно с достаточной точностью представить в виде

Соответствующая (6.31) ЛАЧХ контура регулирования в области низких и средних частот совпадает с прямой 1 (рис.6.18), а в области высоких частот представляется асимптотой 3, имеющей наклон -40 дБ/дек. Частота сопряжения для этой асимптоты 1/Tm расположена ближе к частоте среза, чем и учитывается определяемое (6.29) влияние всех малых постоянных на динамические свойства контура регулирования.
Таким образом, доказано, что при выполнении определенных условий свойства контура регулирования с приемлемой для инженерной практики точностью при последовательной коррекции определяются передаточной функцией (6.31), имеющей второй порядок.
При этом передаточная функция замкнутого контура регулирования будет иметь вид

а корни характеристического уравнения равны:

где а=T0/Tm - соотношение постоянных контура регулирования. При а<4 движение электропривода в переходном процессе при скачке задания и нулевых начальных условиях определяется следующим уравнением:

Суммарная некомпенсируемая постоянная Tm полностью определяет быстродействие электропривода по показателю общего времени переходного процесса tпп. В соответствии с (6.32) свободные составляющие переходного процесса затухают в течение времени

Колебательность электропривода аналогично разомкнутой линеаризованной системе определяется соотношением постоянных контура а; этот же показатель определяет перерегулирование. Следовательно, подбором соотношения постоянных а можно обеспечить требуемые динамические показатели при быстродействии, ограниченном уровнем суммарной некомпенсированной постоянной времени Тm.
Изложенное составляет основу широко используемого в практике электропривода инженерного метода синтеза контуров регулирования координат электропривода. Задавшись требуемым соотношением постоянных а и определив по (6.30) Тm , можно записать желаемую передаточную функцию разомкнутого контура:

передаточная функция объекта регулирования имеет вид:

Передаточная функция регулятора в соответствии с (6.24) определяется так:

Рассматривая (6.36), можно убедиться, что передаточная функция регулятора по мере увеличения числа компенсируемых постоянных l усложняется. При l=0 (все Ti малы) она принимает вид

где Tи=(k,k2...kn)aTm.
В этом случае регулятор представляет собой интегратор с постоянной интегрирования Ти (И-регулятор). При l=1

т е. требуется пропорционально-интегральный регулятор (ПИ-регулятор). При l=2 необходим пропорциональный интсгро-дифференциальный регулятор (ПИД-регулятор) и с дальнейшим увеличением l в его передаточной функции требуется двухкратное и большей кратности дифференцирование входного сигнала.

В структуре на рис.6.19,а в контуре регулирования х3 требуется, чтобы имелась компенсация трех больших и средних постоянных T1, Т2, Т3 и регулятор Wpx3(1) при одноконтурной системе в передаточной функции содержал бы дифференцирующую составляющую второго порядка В соответствии с (6.36) при этом

Рассмотрим, как повлияет на регулирование координаты х3 введение двух вспомогательных контуров регулирования переменных х1 и х2 (рис.6.19,б) Для этого вначале определим передаточную функцию регулятора внутреннего контура регулирования переменной x1 пользуясь изложенным методом.
Для первого контура желаемая передаточная функция

Передаточная функция объекта регулирования переменной x1

Определяем передаточную функцию регулятора:

где Tи1=k1a1Tm
Как и требовалось, получен ПИ-регулятор. Передаточная функция замкнутого первого контура

С учетом (6.42) передаточная функция объекта регулирования переменной х2 принимает вид

Если выбрать a1 таким образом, чтобы внутренний контур представлял собой высокодемпфированное звено, (6.43) можно существенно упростить. Выполненные расчеты и практика настройки регулируемых электроприводов показывают, что без большой погрешности для оценки качества регулирования в знаменателе (6.42) при переходе к (6.43) можно отбросить член второго порядка, при этом

Объект регулирования переменной х2 наглядно представлен на рис.6.19,в. Здесь показано, что в результате введения первого контура из второго контура регулирования исключена большая постоянная T1, а оценка некомпенсированных инерционностей второго контура принимает значение Тm2=а1Тm. Соответственно желаемая передаточная функция для второго контура запишется в виде

передаточная функция регулятора х2 получается путем деления (6.45) на (6.44):

где Тн2=k2a2a1Tm. Вновь получена передаточная функция ПИ-регулятора. Передаточная функция замкнутого второго контура

Выбором а2 и здесь обеспечиваются свойства высокодемпфированного колебательного звена, что при переходе к регулированию основной координаты х3 позволяет представить передаточную функцию объекта регулирования в упрощенном виде:

Структурная схема внешнего контура регулирования переменной х3 при введении двух вспомогательных контуров регулирования, как показано на рис.6.19,г, претерпевает существенные изменения. Сравнивая рис.6.19,г с рис.6.19,a, можно установить, что в результате введения контуров регулирования х1 и х2 на динамику внешнего контура в пределах линейности системы исключено влияние больших постоянных времени T1 и Т2. Однако при этом изменилась суммарная некомпенсированная инерционность контура, оценка которой составляет Tm3=а2а1Тm. Желаемая передаточная функция при этом запишется в виде

Передаточная функция регулятора х3

где Tи3=k3а3а2а1Tm - постоянная времени ПИ-регулятора переменной x3. При принимавшихся по мере решения задачи допущениях передаточная функция замкнутого внешнего контура регулирования приближенно соответствует колебательному звену второго порядка:


Динамические показатели качества регулирования каждой переменной определяются соотношением постоянных а1. На рис.6.20 представлен ряд зависимостей x1=f(t) при различных значениях a1 Если а1=4, переходный процесс имеет апериодический характер, а время регулирования t=tпп=(6¸8)Тm. Уменьшение а1 до а1=2 явно увеличивает колебательность, появляется перерегулирование, при этом время регулирования уменьшается. Дальнейшее уменьшение а, влечет за собой быстрое возрастание колебательности и перерегулирования, а эффект уменьшения /р постепенно снижается. Кривая, соответствующая a1=2, на рис.6.20 выделена утолщенной линией. Это значение соотношения постоянных контура регулирования обеспечивает минимальное время регулирования tр=4,7Tm при практически пренебрежимом перерегулировании Dx1max*=0,043. Такая настройка оптимальна для множества электроприводов, поэтому используется в качестве основной стандартной настройки и называется настройкой на технический оптимум или оптимум по модулю.
При настройке всех контуров регулирования на технический оптимум (аi=2) передаточную функцию i-го разомкнутого контура с помощью (6.45) и (6.49) можно записать так:

То же для замкнутого контура

Следовательно, при прингятых допущениях переходные процессы в i-м контуре при настройке на технический оптимум по характеру совпадают с представленным для а=2 на рис.6.20. Расчетами установлено, что в результате влияния отброшенных в (6.52) и (6.53) членов более высокого порядка при увеличении номера контура i несколько увеличивается перерегулирование и возрастает колебательность. Однако в большинстве случаев это влияние можно полагать пренебрежимо малым. Логарифмические частотные характеристики i-го контура, настроенного на технический оптимум, представлены на рис.6.21. Рассматривая ЛАЧХ, можно убедиться, что с увеличением номера контура i быстродействие уменьшается, так как возрастает некомпенсированная постоянная Тmi и уменьшается частота среза WСi=1/2iТm. Таковы общие характеристики стандартной настройки регулируемого электропривода на технический (модульный) оптимум.
В случаях, когда требуется более высокая точность регулирования, при том же подходе применяют стандартную настройку на симметричный оптимум. При такой настройке желаемую передаточную функцию разомкнутого контура регулирования записывают в виде


Статические характеристики асинхронных двигателей
Для получения выражений статических характеристик с помощью приведенной на рис.3.27,б упрощенной схемы замещения определим вначале ток фазы ротора как функцию параметров двигателя:

где хк=х1 + х2' - индуктивное сопротивление короткого замыкания
Активная электромагнитная мощность, передаваемая через воздушный зазор ротору двигателя, может быть записана в виде

или же через электромагнитный момент и скорость поля двигателя:

Приравнивая (3.74) и (3.75), получаем уравнение статической механической характеристики двигателя в виде зависимости

Анализ функции (3.76) показывает, что она имеет точки экстремума; критическое скольжение, соответствующее экстремуму, может быть определено путем дифференцирования (3.76) по s и последующего приравнивания нулю этой производной:

Подставляя (3.77) в (3.76), получаем выражение критического момента:

С учетом (3.77) и (3.78) уравнение (3.76) может быть после преобразований представлено в форме так называемой уточненной формулы Клосса:

где а=R1/R'2S
Нетрудно видеть, что при s<<sk механическая характеристика близка к линейной зависимости M=2MK·s/sK, а в области больших скольжений (s>>sk) имеет гиперболический характер: М=2MK·sK/s. При s=sk момент принимает максимальные значения, причем в двигательном режиме (SКДВ>0) соответствующее значение критического момента Мкдв, как это следует из (3.78), меньше, чем МК1 генераторном режиме (sKГ <0). С помощью (3.78) можно эту разницу оценить количественно

где |sk| - модуль критического скольжения.

Результирующий поток связан с ЭДС двигателя соотношением

Исходя из выражения электромагнитной мощности, с учетом (3.81) можно записать

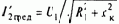 |
Из (3.82) следует, что зависимость момента от скольжения определяется характером изменений потока, тока ротора и соs f2 при изменениях скольжения. Зависимость I'2=f(s) была уже получена [см. (3.73)]. Рассматривая формулу (3.73), можно убедиться, что при возрастании момента в области двигательного режима (s>0) ток ротора монотонно возрастает, стремясь при S®¥ к асимптоте:
В генераторном режиме (s<0) легко обнаруживается максимум:I'2max=U1/xk, соответствующий Sгр=-R'2S/R1=-1/a, причем при s®-¥ ток ротора стремится к той же асимптоте, что и в двигательном режиме. Соответственно зависимость I2(s) имеет вид, показанный на рис.3.29,а.

Зависимость cos ф2 от скольжения (рис.3.29,б) можно получить с помощью схемы замещения рис.3.27,а:

Следовательно, cos f2 при возрастании модуля скольжения монотонно убывает, стремясь при s®¥ к нулю, и зависимость его от скольжения имеет вид, показанный на рис.3.29,б.
Если принять магнитный поток Ф=const, можно прийти к выводу, что в соответствии с (3.82) момент двигателя при малых скольжениях, где cos ф2 изменяется медленно, должен возрастать при увеличении скольжения примерно пропорционально току /2. В области больших скольжений ток I'2 приближается к значению I2пред и изменяется мало, при этом момент, как следует из (3.82), должен снижаться примерно по тому же закону, что и cos f2. Нетрудно видеть, что форма зависимости M=f(s) соответствует изложенному; максимум момента наступает при скольжении, которому соответствует d(I'2 cos f2)/ds=0.
В действительности ЭДС E1 и магнитный поток Фm двигателя при работе в двигательном режиме по мере роста нагрузки и связанного с ним падения напряжения в цепи статора снижаются. Снижение это имеет монотонный характер и добавляется к рассмотренному выше влиянию изменений cos ф2, не меняя характера зависимости M=f(s). Наличие максимума тока в кривой I'2=f(s) в области генераторного режима объясняется тем, что в связи с изменением фазы тока статора и падения напряжения на сопротивлении R1, ЭДС двигателя и поток Ф в области малых скольжений продолжают возрастать и превышают значения, соответствующие идеальному холостому ходу.
При больших скольжениях определяющим становится падение напряжения на сопротивлении x1, здесь ЭДС и поток снижаются аналогично снижению ЭДС и потока в двигательном режиме работы. Этим обусловлены максимум ЭДС и потока в генераторном режиме и соответствующий ему максимум тока ротора. Как следствие, в соответствии с (3.81) максимум момента в генераторном режиме при R1¹0 больше, чем в двигательном.
Естественная механическая характеристика w=f(М) для асинхронного двигателя с фазным ротором представлена на рис.3.30,a. Рабочий участок характеристики, соответствующий wкг>w>wкдв, обладает высокой жесткостью, модуль которой при М<Мном практически постоянен, а при Мном< М<Мк с возрастанием момента двигателя постепенно уменьшается и при w=wк становится равным нулю. Дальнейшее снижение скорости приводит к уменьшению электромагнитного момента, что соответствует изменению знака статической жесткости Рст, которая становится положительной. Этот участок характеристики вплоть до w=0 обычно для двигателей с фазным ротором не используется, и форма характеристики в этой области для таких двигателей существенного значения не имеет. Как показано на рис.3.30,а, двигательному режиму работы соответствуют скольжения от s=1 до s=0.

Область w>w0 (s<0) соответствует генераторному режиму работы параллельно с сетью. При w0<w<wкг подводимая к двигателю механическая энергия частично теряется в двигателе в виде теплоты, а в основном отдается в сеть. Однако при дальнейшем возрастании скорости и соответствующем увеличении частоты тока ротора происходит постепенное уменьшение коэффициента мощности двигателя, который при s=srp становится равным нулю.
При скорости wгр, соответствующей sгр, отдаваемая в сеть активная мощность равна нулю, т.е. вся подведенная к двигателю механическая энергия теряется в виде теплоты в двигателе. Поэтому при w0<w<wгр имеет место режим рекуперативного торможения, при w=wгр наступает режим динамического торможения, а при w>wгр двигатель начинает потреблять энергию из сети, как и при режиме противовключения.
Максимальное значение момента двигателя в двигательном режиме определяет его перегрузочную способность. При этом необходимо иметь в виду, что Мк зависит от квадрата приложенного напряжения U1, вследствие чего асинхронный двигатель весьма чувствителен к колебаниям напряжения сети. В каталожных данных для асинхронных двигателей указывается перегрузочная способность двигателя при номинальном напряжении l=МК/МНОМ . При определении момента допустимой перегрузки следует учитывать возможное снижение напряжения сети на 10%:

Электромеханические естественные характеристики асинхронного двигателя w=f(I1) и w=f(I'2) показаны на рис.3.30,б. Зависимость w=f(I'2) построена с помощью (3.73) и соотношения w=w0(1 - s) (сплошная кривая). В ней отражены все рассмотренные выше особенности зависимости I'2=f(s) (рис.3.29,а) Кривая w=f(I1) в основном повторяет форму кривой w=f(I'2), так как определяется соотношением


Рассматривая эти характеристики, можно установить, что введение добавочных активных сопротивлений в цепь ротора при пуске двигателя и при торможении противовключенисм является эффективным средством ограничения тока и повышения момента двигателя. Переключением сопротивлений можно обеспечить работу двигателя во всех режимах в пределах рабочего участка механических характеристик. В частности, плавным уменьшением сопротивления R'2доб при торможении противовключением и последующем пуске в противоположном направлении можно обеспечить постоянство тормозного и пускового моментов двигателя в этих режимах.
Модуль жесткости рабочего участка механической характеристики при введении сопротивления находится при данном М в обратно пропорциональной зависимости от R'2S, поэтому реостатные характеристики двигателя при больших добавочных сопротивлениях имеют невысокую жесткость.
Искусственные характеристики, соответствующие изменению хк, которое может быть достигнуто введением добавочных индуктивных сопротивлений в цепь статора или ротора, представлены на рис.3.31,д. В соответствии с (3.77) и (3.78) увеличение хк приводит к уменьшению sk и Мк, этим и объясняется форма указанных характеристик. Заметим, что последовательное введение в силовую цепь двигателя емкостного сопротивления позволяет снижать xk и вследствие этого увеличивать перегрузочную способность двигателя. Однако на практике эта возможность в связи с трудностями реализации используется редко.
Характеристики, показанные на рис.3.31,б, дают представление и о форме искусственных механических характеристик, которые могут быть получены введением добавочных активных сопротивлений в цепь статора R1доб. Как это следует из соотношений (3.77) и (3.78), этот параметр влияет на sk и Мк аналогично влиянию хк
Несколько подробнее необходимо остановиться на влиянии на электромеханические свойства асинхронного двигателя изменений напряжения и частоты тока, подводимого к его статору. В пределах рабочего участка механической характеристики, когда ток статора не превышает существенно номинальное значение, ЭДС двигателя E1 незначительно отличается от напряжения сети, поэтому можно приближенно записать
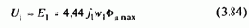
Из (3.84) следует, что при неизменной частоте (f1=const) изменения напряжения приводят к соответствующим изменениям магнитного потока двигателя. Так как в номинальном режиме магнитная цепь двигателя насыщена (рис.3.32), то повышение напряжения сверх номинального приводит при прочих равных условиях к быстрому возрастанию тока намагничивания Im. У двигателей нормального исполнения ток холостого хода I0»Im0»(0,25¸0,35)·I1ном, поэтому повышение напряжения на 20-30% может увеличивать ток холостого хода до значений, превышающих номинальный ток I1ном, и двигатель может нагреваться этим током сверх допустимой температуры даже при отсутствии полезной нагрузки на его валу. При тех же условиях снижение напряжения вызывает в соответствии с (3.84) уменьшение магнитного потока.
Следовательно, напряжение, приложенное к обмоткам статора асинхронного двигателя, при f1=const может рассматриваться как управляющее воздействие, определяющее поток двигателя, так же как и напряжение Uв, приложенное к обмотке возбуждения двигателя постоянного тока. Форма механических характеристик при f1=const и U1=var показана на рис.3.31,в. Она определяется соотношениями (3.77) и (3.78), из которых следует, что скольжение sk при этом остается неизменным, а критический момент уменьшается пропорционально квадрату напряжения.

При необходимости уменьшения частоты f1<f1ном для снижения скорости w0< wном необходимо дополнительно изменять напряжение питания U1 таким образом, чтобы поток поддерживался примерно постоянным Соответственно наиболее эффективные возможности управления асинхронным двигателем обеспечиваются использованием в качестве управляющего воздействия в канале регулирования скорости частоты f1 а в канале регулирования потока напряжения U1.
Приведенный анализ основан на предположении, что при данной механической характеристике в любой ее точке параметры двигателя R1, R'2, x1, х'2 остаются неизменными. Известно, что это допущение вполне приемлемо в пределах рабочего участка механической характеристики, а при s>sk является в большинстве случаев грубым. При больших токах сказывается насыщение зубцов, что вызывает уменьшение индуктивного сопротивления рассеяния. С возрастанием частоты тока ротора существенно проявляется эффект вытеснения тока, вызывающий увеличение активного сопротивления роторной обмотки R'2. Для двигателя с фазным ротором, которым можно управлять таким образом, чтобы во всех режимах обеспечивалась работа в пределах рабочего участка его характеристик, указанные изменения параметров не имеют существенного значения. В наиболее массовом варианте асинхронного электропривода с короткозамкнутым ротором двигателя влияние изменений параметров весьма существенно и его необходимо иметь в виду.
Схема включения асинхронного короткозамкнутого двигателя приведена на рис.3.33,a, а варианты статических механических характеристик показаны на рис.3.33,б. В отличие от двигателя с фазным ротором пуск короткозамкнутого двигателя осуществляется в большинстве практических случаев прямым включением его обмотки статора в сеть, а для торможения используется режим противовключения Поэтому область механической характеристики при s>sК имеет для такого двигателя важное значение и определяет его пусковые и тормозные возможности. Момент Мп, развиваемый двигателем при w=0 (s=1), является важным показателем, включаемым в число каталожных данных двигателя в виде величины Мп/Мном.
Практически при оценке пускового момента следует учитывать возможность понижения напряжения сети на 10% при снижении каталожного значения Мп на 20%. Кроме того, для короткозамкнутых двигателей в каталогах указывается кратность пускового тока I1п/I1ном.
Для сокращения длительности переходных процессов пуска и торможения желательно увеличивать пусковой и тормозной моменты, а для уменьшения нагрузок на сеть полезно ограничивать пусковые и тормозные токи двигателя. Если двигатель имеет ротор с круглыми пазами, то изменения сопротивления роторной обмотки, обусловленные эффектом вытеснения тока, хотя и вызывают отклонения формы механической характеристики от определяемой (3.79), но не обеспечивают значительного увеличения пускового и тормозного моментов и заметного ограничения соответствующих токов (см. кривую 7 на рис.3.33,б). Изготовление двигателя с увеличенным сопротивлением роторной клетки дает модификацию, называемую двигателем с повышенным скольжением (штриховая кривая 2 на рис.3.33,б). При этом достигается увеличение пускового и тормозных моментов, но понижается жесткость рабочего участка механической характеристики, снижается номинальная скорость и возрастают потери в роторной цепи двигателя:
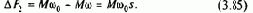

Соотношение (3.85) свидетельствует о том, что потери в роторной цепи при М=const пропорциональны скольжению. Двигатели с повышенным скольжением имеют номинальное скольжение shom=0,04¸0,12, что в 2-3 раза превышает номинальное скольжение того же двигателя нормального исполнения. Соответственно возрастают номинальные потери двигателя, что вынуждает при прочих равных условиях снижать допустимый по нагреву (т.е. номинальный) момент и номинальную мощность двигателя. Увеличение потерь в роторной цепи вызывает также снижение КПД двигателя, поэтому обычно двигатели с повышенным скольжением в установках, работающих длительно с номинальной нагрузкой, не используются.
Более сильно зависит от скольжения активное сопротивление двигателей с глубоким пазом (кривая 3) и особенно с двойной беличьей клеткой (кривая 4 на рис.3.33,б).Сопротивление роторной обмотки таких двигателей в номинальном режиме невелико, но сильно увеличивается при возрастании частоты тока ротора в пусковых режимах и режиме противовключения. Подбором параметров двойной клетки удается обеспечить практическое постоянство момента двигателя в переходных процессах и в то же время обеспечить высокую жесткость рабочего участка механической характеристики и значения КПД, близкие к двигателям нормального исполнения. Кроме того, увеличение активного сопротивления двойной беличьей клетки при больших скольжениях ограничивает потребляемый двигателем ток.
Статические характеристики двигателя с последовательным возбуждением
При принятой аппроксимации кривой намагничивания (рис.3.16) механическая и электромеханическая характеристики (3.51) и (3.52) при различных токах якоря имеют различные выражения. При Iя<Iгр kф=const и эти уравнения преобразуются к виду

При Iя>Iгр Ф=Фнас=const и те же уравнения записываются так:

Уравнения (3.53) и (3.54) свидетельствуют о том, что в области нагрузок, меньших номинальной, статические характеристики двигателя с последовательным возбуждением имеют гиперболический характер и при М®0 и Iя®0 асимптотически приближаются к оси ординат. Эта форма характеристики определяется условиями электрического равновесия машины: при идеальном холостом ходе (IЯ=0) ЭДС двигателя должна уравновешивать приложенное к якорной цепи напряжение Uя. Так как при Iя®0 поток Ф также стремится к нулю, выполнение условия


При Iя>Iгр магнитная цепь машины насыщается и при принятом допущении Ф=Фнас=const. В этой области характеристики двигателя практически линейны, подобно аналогичным характеристикам двигателя с независимым возбуждением.
Естественные характеристики двигателя с последовательным возбуждением показаны на рис.3.17,a,б. Сильная положительная связь по току, создаваемая последовательной обмоткой двигателя, практически устраняет влияние размагничивающего действия реакции якоря и приводит в области допустимой перегрузки к возрастанию потока сверх номинального значения на 10-15%. Поэтому при том же коэффициенте допустимой перегрузки по току lI=2¸2,5 перегрузочная способность по моменту у двигателей с последовательным возбуждением выше, чем при независимом возбуждении, и лежит в пределах lI=2,5¸3.
Форма естественной механической характеристики определяет область применения двигателя с последовательным возбуждением. Он наиболее часто применяется в электроприводе механизмов, для которых желательно, чтобы по мере снижения нагрузки до минимальной, скорость движения возрастала в 1,5-2 раза, обеспечивая соответствующее повышение производительности при данной мощности двигателя. При этом важным достоинством двигателя является повышенная перегрузочная способность.
В связи с нелинейностью кривой намагничивания рассчитать естественные характеристики двигателя с последовательным возбуждением только по его номинальным данным не представляется возможным. Поэтому в каталогах приводятся естественные характеристики w=f(Iя) и М=f(Iя), которые и следует использовать при проектировании электроприводов с двигателями последовательного и смешанного возбуждения. Для ориентировочных или учебных расчетов можно пользоваться универсальными характеристиками, приведенными в примере 3.4.

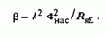

Статические характеристики двигателя, соответствующие различным значениям напряжения питания, приведены на рис.3.18.
Их вид свидетельствует о том, что уменьшение напряжения приводит к снижению скорости при данной нагрузке без изменения соответствующей этой нагрузке жесткости механической характеристики.
Механическая характеристика при Uя= 0 соответствует режиму динамического торможения двигателя при замкнутой накоротко его якорной цепи. В данном случае торможение протекает при самовозбуждении, поэтому его особенности заслуживают дополнительного рассмотрения.
В общем случае при питании двигателя от сети с постоянным напряжением Uя=UHOM для осуществления режима динамического торможения его якорная цепь отключается от сети и замыкается на внешний резистор Rдоб (рис.3.19,а), Если с помощью внешнего источника механической энергии (например, при наличии движущей активной нагрузки) привести якорь двигателя во вращение, то при выполнении определенных условий двигатель самовозбуждается и развивает зависящий от скорости тормозной момент.
Первым условием самовозбуждения является наличие остаточного потока такого знака, чтобы при данном направлении вращения ЭДС, наводимая остаточным потоком, вызвала ток возбуждения, увеличивающий поток двигателя. Если двигатель работал в двигательном режиме при w>0, то его ЭДС в режиме торможения при w>0 создает ток, направленный противоположно току якоря в предшествующем режиме. Этот ток, протекая по обмотке возбуждения, создает МДС, уменьшающую поток остаточного намагничивания, и самовозбуждение исключается. Если при этом изменить направление вращения (w<0), двигатель самовозбудится, поэтому характеристика на рис.3.18 при Uя=0 существует только в четвертом квадранте. Обеспечить торможение во втором квадранте можно, переключив либо выводы якоря, либо выводы обмотки возбуждения.
Второе условие самовозбуждения поясняет рис.3.19,б. Здесь приведен ряд зависимостей E(Iя), соответствующих различной скорости движения якоря. Если воспользоваться кусочно-линейной аппроксимацией кривой намагничивания, показанной на рис.3.16, зависимости Е(IЯ) приближенно линеаризуются, причем при Iя>Iгр ЭДС принимается приближенно постоянной. На рис.3.19,б показана также прямая Iя=f(E)=Е/RяS Известно, что при самовозбуждении E(Iя)=Iя(E), и второе условие самовозбуждения графически выражается наличием точки пересечения этих характеристик.
Это условие на рис.3.19,б выполняется только при w>w2, причем граничное значение скорости wгр»w3. Таким образом, самовозбуждение может наступить только после достижения скорости wгр при которой наклон линейной части характеристики Е(Iя) совпадает с наклоном прямой Iя=Е/RЯS. Следовательно, при увеличении суммарного сопротивления цепи якоря самовозбуждение наступает при более высоких скоростях wгр.
Изложенные соображения позволяют установить форму характеристики динамического торможения с самовозбуждением, показанную на рис.3.19,в. При w<wгр самовозбуждение отсутствует и IЯ»0. При w=wгр двигатель самовозбуждается, ток якоря при принятой аппроксимации возрастает до Iя=Iгр и при дальнейшем увеличении скорости двигатель имеет линейную характеристику w(Iя), соответствующую Ф=Фнас=const. Поэтому при принятой идеализации электромеханическая характеристика при динамическом торможении с самовозбуждением имеет вид ломаной 1 на рис.3.19,в.
В связи с наличием остаточного потока Фост ток при w<wгр несколько возрастает, а реальная форма кривой намагничивания приводит к дополнительным отклонениям фактической кривой w(Iя) (кривая 2 на рис.3.19,в) от приближенной кривой 1. Форма механической характеристики в этом режиме аналогична форме электромеханической характеристики 2. В этом можно убедиться, рассмотрев приведенные на рис 3.19,г механические характеристики динамического торможения с самовозбуждением при различных добавочных сопротивлениях в цепи якоря.
Статические характеристики и динамические
В связи с развитием регулируемого асинхронного электропривода с частотным управлением значительный практический интерес представляет изучение свойств асинхронного электромеханического преобразователя при питании от источника тока. Это обусловлено тем, что значительная часть используемых преобразователей частоты обладает свойствами источника тока, т. е. формирует в фазах двигателя токи, которые не зависят от режима работы и параметров двигателя, а определяются только сигналом задания. Схема включения двигателя для этого случая показана на рис.3.39. В этой схеме двигатель получает питание от трехфазного источника тока. Значение тока определяется напряжением задания тока мзт, а частота - напряжением мзч.

Так как в схеме рис.3.39 обмотки статора питаются неизменным током, уравнения механической характеристики (3.64) запишутся в виде

потокосцепления в (3.97) могут быть выражены через токи:

Подставив в уравнение для обмотки 2х выражения потокосцеплений (3.98), определим ток фазы 2у.

где
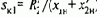
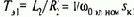
Система (3.97) нелинейна, поэтому при преобразованиях необходимо соблюдать условия, отмеченные в §3.12. Подставим (3.99) в уравнение для обмотки 2у и с соблюдением указанных условий преобразований разрешим его относительно тока фазы 2х:

Искомое уравнение механической характеристики асинхронного электромеханического преобразователя при питании от источника тока получим, подставив (3.100) в последнее уравнение системы (3.97)

здесь Мк1 - критический момент при питании от источника тока. В переменных двухфазной модели он получен в виде

Уравнение критического момента для трехфазной машины получим, заменив максимальное значение тока двухфазной модели I1max действующим значением тока фазы трехфазного двигателя I1 с помощью формулы (2.37):
Кривая намагничивания представлена на рис.3.41,б, там же построена кривая х=f(I), соответствующая данной кривой намагничивания. Для анализа формы статических характеристик с приближенным учетом насыщения характеристика Фm=f(Im) аппроксимирована двумя прямыми. При Im<Imнас магнитная цепь машины ненасыщена и xm=xmн=const (прямая 1). Если Im>Imнас, насыщение сказывается существенно и приближенно можно принять Фm=Фцнас=const (прямая 2 на рис.3.41,б).
Так как Im<I1 то при Im<Imнас магнитная цепь двигателя при любых скольжениях не насыщается и х=const. В этой области значений I1 статические механические характеристики двигателя описываются уравнением (3.101) при р=0:

где

На рис.3.42,а представлено семейство характеристик w=f(М), соответствующих ряду значений частоты f1 при Im£Imнас. Так как зависимость M=f(sa) (3.109) инвариантна относительно частоты, то при изменении f1 изменяется только скорость идеального холостого хода w0=2pf1/pп, а форма механических характеристик относительно этой точки не претерпевает изменений. Особенностью этих характеристик является малость критического скольжения sK1, по сравнению с sk, соответствующим питанию от источника напряжения, обусловленная тем, что хmн>>х1н+х'2н.
Однако при I1£Imнас невелико и значение Мк1. Поэтому для получения требуемой перегрузочной способности, аналогичной перегрузочной способности на естественной характеристике, в режиме питания от источника тока необходимо выбирать значения

При I1>>Imнас и идеальном холостом ходе магнитная цепь машины находится в глубоком насыщении, поэтому при малых значениях sa можно без большой погрешности принять Ф =Фmнас=const. С ростом скольжения намагничивающий ток Im уменьшается, однако в соответствии с принятой аппроксимацией до значения sa=sa.rp, при котором Im=Imнас, насыщение сохраняется. В области больших скольжений (sa> sa.rp), как показано на рис.3,41,a ток Im<Imнас, хm возрастает и приближенно может быть принято равным хmн (рис.3.41,б).
Отсюда следует, что при I1>>Imнас в области sa<sa.rp реальная форма кривой w=f(М) в значительной мере отклоняется от определяемой (3.109), а при больших скольжениях (sa> sarp) магнитная цепь размагничивается током ротора и реальная механическая характеристика сближается с рассчитываемой по (3.109). Принятая аппроксимация кривой намагничивания позволяет приближенно оценить вид механической характеристики при насыщении, которое соответствует области малых скольжений, т. е. рабочему ее участку. При насыщении Фm=Фmнас=const и ЭДС Е'2 при w0ном достигает значений, близких к U1ном. С учетом этого для режима насыщения можно принять E'2=U1ном=const и представить (3.109) в виде

где

Следовательно, насыщение смещает максимум момента в область больших скольжений, так как sk1нac>sk1.
Проведенный анализ влияния насыщения позволяет представить реальную форму механических характеристик при различных значениях I1. На рис.3.42,б приведены механические характеристики 1-3, соответствующие токам I11=Imнас, I12>Imнас И I13>I12, которые построены по (3.109) без учета насыщения. Там же показана механическая характеристика 4 для насыщенного состояния магнитной цепи, определяемая (3.110). Реальные механические характеристики (кривые 5-7) в области насыщения (sa<sа.гр) совпадают с кривой 4, а при отсутствии насыщения (sa>sа.гр) приближаются к соответствующим кривым 1-3.
Граничное скольжение sа.гр при I1=I11 равно нулю и с возрастанием тока I1 увеличивается. Соответственно при I11=Imнас магнитная цепь машины не насыщается при любых скольжениях и кривая 1 сливается с соответствующей реальной характеристикой 5. С увеличением I1 и возрастанием sагр увеличивается зона, где механические характеристики совпадают с кривой 4, а зона, в которой они совпадают с рассчитываемыми без учета насыщения, постепенно сокращается. Это, как видно на рис.3.42,б, приводит к постепенному увеличению критического скольжения.
Сравнивая уравнение механической характеристики для динамических процессов (3.101) с уравнением (3.92), соответствующим питанию двигателя от источника напряжения, можно установить, что они совпадают по форме и отличаются лишь выражениями критического момента и электромагнитной постоянной времени.
Следовательно, выполнив линеаризацию уравнения (3.101) в окрестности точки М°=0, s°а= 0 аналогично линеаризации, выполненной для уравнения (3.92), получим приближенное линеаризованное уравнение механической характеристики в виде

где b1=2Мк1/w0ном·sk1.
Передаточная функция динамической жесткости

Структурная схема электромеханического преобразования энергии при питании от источника тока в соответствии с (3.111) совпадает с полученной выше схемой для питания от источника напряжения и приведенной на рис.3.38. Однако динамические свойства в этих режимах существенно различны в связи с тем, что при питании от источника тока поток при I1=const изменяется в широких пределах. Изменения главного потока машины при этом определяют существенно большую инерционность электромеханического преобразователя, чем при питании от источника напряжения. Действительно, сравнивая

можно убедиться, что Тэ<<Тэ1 С ростом тока статора вследствие насыщения индуктивное сопротивление намагничивания х уменьшается, при этом уменьшается и электромагнитная постоянная Tэ1, стремясь при больших насыщениях к Тэ.
В отличие от питания от источника напряжения при питании от источника тока можно изменять частоту, не изменяя сигнала задания тока. Однако практически и в этом случае для обеспечения определенных условий протекания процессов электромеханического преобразования энергии задание тока в схеме рис.3.39 изменяют в функции задания частоты по тем или иным законам частотного управления.
Структура и характеристики линеаризованного электромеханического преобразователя
Уравнения механической характеристики двигателя (2.25) с помощью выражений для потокосцеплений (2.20) можно представить в виде (здесь р=d/dt)

Уравнениям (2.38) соответствует структура преобразователя, представленная на рис.2.7. Здесь напряжения u1м, u1v, и2u, u2v есть преобразованные управляющие воздействия, связывающие двигатель с системой управления. Значение скорости w вводится в структуру электромеханического преобразователя из структурной схемы механической части электропривода и отражает реальную электромеханическую связь, в результате которой развиваемый двигателем момент М зависит от условий движения механической части. Выходом структурной схемы преобразователя является электромагнитный момент М, который для механической части (см. гл. 1) представляет собой управляющее воздействие.

При изучении динамических свойств электромеханических преобразователей и систем электропривода используется общий прием исследования нелинейных систем - линеаризация уравнений механической характеристики. С этой целью система уравнений преобразуется к одному нелинейному уравнению, связывающему момент и скорость машины в динамических процессах, и осуществляется разложение этого уравнения в ряд Тэй-лора в окрестности точки статического равновесия. В результате преобразований линеаризованное уравнение механической характеристики приводится к виду

где w(p), М(р), и(р) - изображения по Карсону механических переменных и управляющего воздействия; а(р), b(р), с(р) - операторные коэффициенты при соответствующих переменных.
Для получения структурной схемы линеаризованного преобразователя, аналогичной исходной схеме рис.2.7, необходимо решить уравнение (2.39) относительно момента:

Уравнение (2.40) устанавливает аналитическую связь между электромагнитным моментом машины М(р), угловой скоростью ротора w(р) и управляющим воздействием и(р).


Структура линеаризованного электромеханического преобразователя, соответствующая уравнению механической характеристики (2.39), представлена на рис.2.8,a. Сравнивая рис.2.7 и 2.8,a, можно наглядно представить, в какой степени упрощается анализ динамических свойств преобразователя при линеаризации.
Если решить уравнение (2.39) относительно скорости можно установить, что при идеальном холостом ходе двигателя, когда М(р)=0,
Известно, что скорость идеального холостого хода для машин постоянного тока определяется приложенным напряжением ия(р), а для машин переменного тока - частотой приложенной системы напряжений, которой пропорциональна угловая скорость поля. Поэтому в наиболее общем виде уравнение механической характеристики линеаризованного электромеханического преобразователя может быть представлено так:


Уравнению (2.42) соответствует структурная схема рис.2.8,б. Эта структура показывает, что изменения скорости электропривода для электромеханического преобразователя являются возмущениями, определяющими изменения электромагнитного момента при данном управляющем воздействии. Передаточная функция электромеханического преобразователя по возмущению называется динамической жесткостью механической характеристики:
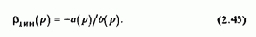
Динамическая жесткость механической характеристики (2.43) позволяет анализировать реакцию электромеханического преобразователя на изменения скорости во всех режимах работы на основе частотного метода теории автоматического управления. Уравнение АФХ динамической жесткости

определяет зависимость модуля динамической жесткости от частоты колебаний W

и сдвиг по фазе между колебаниями момента и скорости yb(W). Статическому режиму работы (р=0) электромеханического преобразователя соответствует модуль статической жесткости

а фаза yb(0)=-p. В этом можно убедиться, записав (2.42) для статического режима (р=0):

Продифференцировав (2.47) по скорости, получим

Модуль статической жесткости механических характеристик электропривода р показывает, как изменяется момент двигателя при изменениях скорости, обусловленных изменениями статической нагрузки в механической части электропривода. В теории электропривода этот показатель имеет весьма важное значение, так как требования к жесткости механических характеристик в различных режимах работы определяются технологическими требованиями к электроприводу со стороны приводимой в движение машины. Частотные характеристики динамической жесткости (2.43) позволяют оценивать, в какой полосе частот для анализа режимов работы электропривода можно пользоваться статическими механическими характеристиками. Кроме того, они характеризуют точность поддержания установленных значений скорости или момента в динамических процессах работы электропривода.
Механические статические характеристики и частотные характеристики динамической жесткости в дальнейшем изложении используются в качестве основного инструмента для анализа электромеханических свойств различных двигателей и систем электропривода.
Связь показателей регулирования с ЛАЧХ разомкнутого контура регулирования
Математические методы теории автоматического управления являются основой для синтеза замкнутых систем регулируемого электропривода с заданными статическими и динамическими показателями. Наиболее общие и широко используемые на практике представления о возможностях реализации заданных показателей регулирования дает известная из курса теории управления связь основных показателей с ЛАЧХ разомкнутого контура регулирования.


где Wpx и Wopx - передаточные функции соответственно регулятора величины х и объекта регулирования; W''opx - передаточная функция объекта регулирования по возмущающему воздействию FB.
Если для рассматриваемого контура регулирования определить передаточные функции ошибки по управлению хз и по возмущению FB то с их помощью можно получить известное из теории управления изображение суммарной ошибки замкнутого контура регулирования:

Пусть в общем случае передаточная функция разомкнутого контура регулирования имеет вид

где v - порядок астатизма контура; m, п - число последовательно включенных соответственно инерционных и форсирующих звеньев; k - коэффициент усиления разомкнутого контура.
Для того чтобы после замыкания контура отрицательной обратной связью по регулируемой координате обеспечивались требуемая точность и динамические показатели качества регулирования, ЛАЧХ разомкнутого контура должна иметь вполне определенный вид и параметры. Общая форма желаемой ЛАЧХ разомкнутого контура представлена на рис.6.17.

Для получения требуемой точности необходимо предусмотреть коэффициент усиления, отвечающий условию
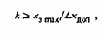
где х3 max - заданное значение переменной; Dхдоп - допустимая ошибка регулирования.
Если требуется исключить статическую ошибку по заданию, необходимо, чтобы в контуре был интегрирующий элемент (v=1), при этом будет иметься динамическая ошибка, возникающая при изменениях задания Увеличение порядка астатизма (v=2) повышает при надлежащем коэффициенте усиления k динамическую точность регулирования.
Низкочастотная часть желаемой ЛАЧХ, соответствующая v=0, 1,2, представлена на рис.6.17 в виде отрезков прямых 1-3 Нетрудно видеть, что повышение порядка астатизма увеличивает значения комплексного коэффициента усиления в низкочастотной части и динамическая точность регулирования возрастает тем в большей степени, чем в более широком диапазоне частот обеспечивается повышение амплитуд.
Динамические показатели качества регулирования определяются главным образом среднечастотной асимптотой ЛАЧХ Lраз х.
Для получения достаточного запаса устойчивости необходимо, чтобы в районе частоты среза Wc. был достаточно протяженный участок с наклоном -20 дБ/дек. Чем шире этот участок, тем выше на частоте среза запас по фазе DY(WС)=-p-Y(WC), где Y(W) - ФЧХ контура. Зависимость DY(W) показана на рис.6.17 (кривая 4).
От запаса по фазе на частоте среза зависят колебательность и перерегулирование (см. рис.6.3):

Частота среза определяет быстродействие контура регулирования. С ней связано время регулирования

а также время максимума перерегулирования

Ближайшая нижняя частота сопряжения W1H влияет на перерегулирование: по мере приближения W1н к частоте среза запас по фазе DY(WС) уменьшается и перерегулирование возрастает. Ближайшая к частоте среза верхняя частота сопряжения W1B и вся высокочастотная часть ЛАЧХ Lpa3x сказывается на начальном участке переходного процесса.
Чем ближе частоты сопряжения этой области к частоте среза и чем выше наклон удаленной асимптоты, тем больше показанный на рис.6.3 участок запаздывания движения t3.
Таким образом, требования к точности и динамическим показателям электропривода при регулировании определенной переменной позволяют конкретизировать количественные характеристики желаемой ЛАЧХ разомкнутого контура. При известной ЛАЧХ объекта регулирования переменной х Lopx желаемая ЛАЧХ разомкнутого контура Lразх позволяет определить требуемую ЛАЧХ регулятора, вводимого в контур регулирования:

Далее решается техническая задача подбора удобной схемы регулятора и определения его параметров, исходя из (6.23). Этот путь синтеза универсален и позволяет наиболее полно учесть весь комплекс предъявляемых к электроприводу требований в отношении как точности регулирования, так и его динамических показателей в наиболее сложных случаях.
Однако при проектировании электроприводов массового применения, при создании унифицированных систем электропривода широкого назначения этот путь сложен и не обеспечивает достаточной конкретности получаемых динамических свойств регулируемого электропривода.
Для случаев, когда в основу синтеза могут быть положены динамические показатели, в теории электропривода разработан инженерный метод последовательной коррекции с использованием подчиненных контуров регулирования.
Этот метод позволяет получить вполне определенные динамические свойства регулируемого электропривода, соответствующие конкретным так называемым стандартным настройкам контуров регулирования.
Свойства электропривода при настройке контура регулирования скорости на технический оптимум


Следуя рекомендациям, данным в §6.8, пренебрежем в передаточной функции Wзам.м членом, содержащим р2:

Соотношение (8 37) показывает, что для контура скорости некомпенсируемая постоянная времени Tmc=амТm, т.е. в ам раз больше, чем для подчиненного контура регулирования момента. Желаемая передаточная функция для контура регулирования скорости

где ас=TОС/TmС - соотношение постоянных контура скорости. Передаточная функция регулятора скорости

Необходим П-регулятор скорости с коэффициентом kpc. Так как выходное напряжение регулятора скорости является сигналом задания момента uзм для подчиненного контура, необходимо ограничить максимальное значение uзм, исходя из требуемого стопорного момента:
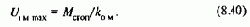
Характеристика UBЫX=f(UBX) регулятора скорости, отвечающая этому условию, представлена на рис.8.13,б. Передаточная функция замкнутого контура регулирования скорости

Выбором соотношения постоянных времени контура в пределах ас=2¸4 можно получить требуемое по техническим условиям демпфирование колебаний скорости в переходных процессах и ограничить перерегулирование допустимым значением. Наиболее широко на практике используется стандартная настройка на технический оптимум ас=ам=2, при этом
Стандартная настройка контура регулирования скорости на технический оптимум широко используется на практике в связи с простотой технической реализации и благоприятным для большинства электроприводов характером протекания переходных процессов. Однако, как было установлено, точность регулирования при малом моменте инерции электропривода может быть ниже, чем в разомкнутой системе электропривода, и не удовлетворять предъявляемым требованиям. В этих случаях в многоконтурных унифицированных структурах регулирования координат электропривода прибегают к увеличению порядка астатизма системы по отношению к воздействию нагрузки.
Одним из возможных путей увеличения точности регулирования скорости при изменениях нагрузки является дополнение двухконтурной системы регулирования скорости, настроенной на технический оптимум, вторым контуром регулирования скорости, настроенным так же, как и первый.
Структурная схема трехконтурной системы с двумя контурами регулирования скорости и подчиненным контуром регулирования момента приведена на рис.8.19,а. Для внешнего контура регулирования скорости объектом регулирования является замкнутый внутренний контур, передаточная функция которого имеет вид


В результате последовательной коррекции необходимо получить следующую передаточную функцию разомкнутого внешнего контура регулирования скорости:

Следовательно, регулятор скорости внешнего контура регулирования должен иметь передаточную функцию интегрирующего звена

Передаточная функция замкнутой трехконтурной системы при настройке на технический оптимум (ас1=ас=ам=2)

С помощью структурной схемы на рис.8.19,а, приняв koс1=k0c, с учетом (8 39) и (8 56) получим выражение динамической жесткости механической характеристики

Асимптотическая ЛАЧХ динамической жесткости, соответствующая (8.58), для настройки на технический оптимум aс1=ас=ам=2 представлена на рис.8.19,б. Сопоставление этой характеристики с аналогичной характеристикой двухконтурной системы (см. рис.8.14) свидетельствует о том, что введение дополнительного контура регулирования скорости обеспечивает астатическое регулирование скорости в области низких частот.

Рассмотрим, какими свойствами обладает электропривод при такой настройке контура регулирования скорости. Благодаря малости некомпенсируемой постоянной времени Т подчиненный контур регулирования момента обеспечивает в области малых и средних частот высокую точность регулирования момента, при которой допустимо пренебречь влиянием электромеханической связи и получить уравнение механической характеристики с помощью структурной схемы на рис.8.13,а при ам=2:

С помощью (8.39) уравнение (8.43) можно представить в виде

где
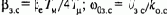

Это уравнение справедливо в пределах линейной части характеристики регулятора скорости, т. е. при (uзс-kосw)/kрс£Uзмmax. При снижении скорости до значения wгр=w0зс-МСТОП/b3с выходное напряжение регулятора скорости достигает максимального значения и при w<wгр М=Мстоп=const. Механические характеристики электропривода при настройке контура регулирования скорости и подчиненного контура регулирования момента на модульный оптимум показаны для различных Тм на рис.8.13,в.
В соответствии с (8.44) модуль жесткости механической характеристики в замкнутой по скорости системе определяется соотношением динамических параметров - постоянных времени ТМ и Тm . Это объясняется выбором коэффициента обратной связи по скорости из условия получения определенных динамических показателей, соответствующих техническому оптимуму. Как следствие, точность регулирования при различных параметрах механической части оказывается существенно различной.

Структурная схема электропривода, соответствующая (8.44), представлена на рис.8.14,а. Определим с ее помощью передаточную функцию динамической жесткости механической характеристики в замкнутой системе:

Соответствующие (8.46) ЛАЧХ при различных отношениях ТМ/4Тm приведены на рис.8.14,б. Там же для сравнения приведена ЛАЧХ динамической жесткости характеристики разомкнутой системы (штриховая прямая 1). Сравнивая их, можно заключить, что при Тэ>2Тm область частот, в которой расхождения между статикой и динамикой невелики, расширяется и точность регулирования также зависит от отношения ТМ/4Тm как и в статике.
В соответствии с (8.38) и схемой на рис.8.14,a изображение ошибки регулирования по управляющему воздействию при ам=ас=2 имеет вид

Положив в (8.47) р=0, можно убедиться, что при w0зс=const статическая ошибка по управляющему воздействию отсутствует, электропривод по управлению обладает астатизмом первого порядка.
Если управляющее воздействие нарастает по линейному закону

то в установившемся режиме будет иметь место постоянная ошибка, определяемая (8.47) при подстановке в эту формулу (8.48) и р=0:

Определим с помощью рис.8.14,a и формулы (6.19) изображение ошибки по возмущению, обусловленному статической нагрузкой электропривода Мс(р):

При р=0 и Мc=const (8.50) определяет статическую ошибку по нагрузке

которая определяется модулем жесткости механических характеристик в замкнутой системе электропривода (см. рис.8.13,в).


С учетом известного характера изменения переменных в переходных процессах при настройке на технический оптимум (8.48) и (8.52) позволяют установить вид зависимостей w(t) и М(t) при линейном нарастании задающего сигнала и Мнач=Мс (рис.8.15). Так как перерегулирование и колебательность при aс=ам=2 пренебрежимо малы, максимум переходной ошибки на р.8.15 незначительно отличается от установившейся динамической ошибки DwзсS.

Если важно минимизировать динамическое падение скорости и допустимо увеличить колебательность электропривода, на практике отступают от настройки на технический оптимум и выбирают при аM=2ас<2, при этом (8.51) можно представить так:

В соответствии с (8.53) при ас<2 возрастает модуль жесткости статической механической характеристики bзс и уменьшается статическая ошибка Dw'3с. Увеличение статической точности регулирования может в определенных пределах быть более существенным, чем возрастание динамических ошибок в связи с повышением колебательности электропривода. В этом можно убедиться, рассматривая рис.8.17, на котором построены для aм=2 зависимости Dwзс* =f(t) при ас=2 (рис.8.17,а) и ас=1 (рис.8.17,б), причем
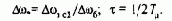

В качестве базового значения ошибки принята статическая ошибка Dw'3cS при аM=2, ас=2.
В области сре- днечастотной асимптоты модуль динамической жесткости остается таким же, как и в двухконтурной системе, что дает основание предполагать, что при быстрых изменениях нагрузки точность регулирования в астатической системе незначительно отличается от динамической точности более простой двухконтурной системы.
Ошибку регулирования по управляющему воздействию определим с помощью передаточной функции разомкнутого контура (8.55):

Трехконтурная система, как и двухконтурная, обладает аста-тизмом первого порядка по управляющему воздействию, причем динамическая ошибка при линейном нарастании задающего сигнала w0зс=e3/p составит
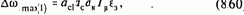
т. е. при добавлении третьего контура увеличивается в 2 раза по сравнению с (8.49). Так наглядно подтверждается отмеченная выше особенность многоконтурных систем подчиненного регулирования - при настройке на технический оптимум некомпенсируемая постоянная возрастает в 2i-1 раз с возрастанием номеpa контура i. Соответственно возрастает и динамическая ошибка регулирования.
При настройке на технический оптимум ac1=aс=aм=2



Как уже было отмечено, трехконтурная система обеспечивает астатическое регулирование и по нагрузке. Установившаяся ошибка при линейном нарастании нагрузки во времени ограничена значением

Таким образом, точность регулирования скорости в статических режимах в трехконтурной системе по сигналу задания сохраняется на том же уровне, что и в двухконтурной системе, а по нагрузке существенно возрастает, так как обеспечивается астатическое регулирование. В установившихся режимах линейного изменения задания ошибка регулирования больше в трехконтурной системе.
Поскольку среднечастотная асимптота ЛАЧХ динамической жесткости в обеих системах одинакова, динамическая точность этих систем примерно одинакова. Характер переходных процессов при изменениях задающего сигнала соответствует настройке на технический оптимум, но быстродействие получается примерно в 2 раза ниже, чем в простейшей двухконтурной системе.
Обеспечить астатизм по нагрузке при регулировании скорости можно без применения второго контура регулирования скорости путем настройки двухконтурной системы на симметричный оптимум. Для реализации этого пути при последовательной коррекции контура регулирования скорости задаются желаемой передаточной функцией разомкнутого контура в виде (6.54), причем в связи с наличием подчиненного контура регулирования момента принимают Тmс=2Тm:

Передаточная функция объекта регулирования при отбрасывании члена второго порядка в передаточной функции замкнутого контура момента имеет вид

Передаточная функция регулятора скорости

Получены передаточная функция ПИ-регулятора скорости и соотношения для расчета его параметров:

Передаточная функция замкнутого контура регулирования скорости по управлению

Для анализа реакции синтезированной системы на изменения нагрузки преобразуем полученную в результате коррекции структурную схему (рис.8.21,а) к виду, представленному на рис.8.21,б. Рассматривая последнюю структуру, можем записать передаточную функцию динамической жесткости механической характеристики замкнутой системы:


Однако точность при отработке сигнала задания выше в двухконтурной системе, настроенной на симметричный оптимум. В соответствии с (8.62) и ЛАЧХ разомкнутого контура, показанной на рис.8.22,б, двухконтурная система с ПИ-регулятором скорости обладает астатизмом второго порядка.
Изображение ошибки регулирования при изменениях управляющего воздействия в такой системе определяется с помощью (8.62):

Уравнение (8.65) показывает, что благодаря астатизму второго порядка установившаяся динамическая ошибка в режимах линейного нарастания задания w0=e3t отсутствует. По этой причине двухконтурную систему с ПИ-регулятором скорости называют двукратноинтегрирующей системой и применяют в тех случаях, когда важно иметь высокую точность отработки изменений сигналов задания.
Наличие в ЛАЧХ разомкнутого контура (рис.8.22,б) низкочастотной асимптоты с наклоном -40 дБ/дек приводит к снижению запаса по фазе на частоте среза W=1/4Tm по сравнению с настройкой на технический оптимум, что определяет значительно большие перерегулирования по скорости при отработке скачка задания, чем в трехконтурной системе.
Установившаяся ошибка при настройке на симметричный оптимум в режимах линейного нарастания задания w3=e3t, как отмечено, равна нулю. Однако в начале процесса в связи с электромагнитной инерцией (8.65) определяет отставание изменения скорости от заданных значений wэ (рис.8.23). Возникшая на этом этапе ошибка отрабатывается в течение времени tp»10·Tm с перерегулированием по моменту М и ускорению e=dw/dt, достигающим 56% установившихся значений Муст=JS·eз (Mc=0) и eуст=eз.


Поэтому в случаях, когда важно повысить жесткость механической характеристики и увеличить статическую точность регулирования при изменениях нагрузки, либо применяют рассмотренную выше трехконтурную структуру, либо корректируют реакцию двухконтурной системы на изменения управляющего воздействия путем введения на вход системы дополнительного звена. В частности, таким путем можно, не изменяя точности по нагрузке, получить настройку системы с ПИ-регулятором скорости по управлению, соответствующую техническому оптимуму. Сравнивая рис.8.20,в для трехконтурной системы с рис.8.21,в для системы с ПИ-регулятором скорости, можно убедиться, что для достижения этой цели необходимо на задающий вход регулятора включить фильтр с передаточной функцией

К этому же выводу можно прийти и путем сравнения передаточной функции замкнутой трехконтурной системы (8.57) с такой же передаточной функцией для настройки на симметричный оптимум в двухконтурной системе. При введении такого звена установившаяся ошибка при линейном нарастании задания уже получается не равной нулю, а определяется (8.60). Характер переходных процессов в системе при этом соответствует настройке на технический оптимум.
Типовые статические нагрузки электропривода
Электромагнитный момент двигателя является выходной величиной для электрической части системы (см. рис.В.2) и входной для механической, поэтому при рассмотрении процессов в системе он выделен из всех действующих на механическую часть внешних моментов. Все остальные силы и моменты определяют статическую нагрузку электропривода Mс. Во всех трех расчетных схемах (рис.1.2) в соответствии с (1.13) эта нагрузка неизменна, так как для двухмассовой системы Mc1 + Мс2=Mс, а для трехмассовой Mс1 + Мс2 + Mс3=Mс. Иными словами, при учете упругости суммарная нагрузка неизменна, но уточняется, к каким массам системы приложены отдельные составляющие нагрузки.
Все силы и моменты нагрузки, приложенные к механической части электропривода, делятся на силы и моменты механических потерь и силы и моменты, представляющие полезные нагрузки исполнительного механизма. Для схемы рис 1.1,б в общем виде можно записать
Mc=DMS+Mпол.S (1.14)
| где: |  |
– суммарный приведенный момент потерь, с учетом момента механических потерь в двигателе; |
р, q - число моментов и сил в системе, представляющих механические потери,
Мпол.S- суммарный приведенный момент полезной нагрузки.

Так как для электропривода имеет важное значение, как зависит момент статической нагрузки от скорости, в дальнейшем используется понятие механической характеристики исполнительного механизма, представляющей собой зависимости Mс=f(w) и w=f(Mс).
По характеру взаимодействия с электроприводом все силы и моменты делятся на активные и реактивные
Активными силами и моментами называются силы и моменты, создаваемые внешними по отношению к двигателю источниками механической энергии независимо от движения электропривода, например потенциальной энергией перемещаемых по вертикали грузов, энергией ветра и т.п.
На рис.1.3, a упрощенно показан подъемный механизм, нагрузкой которого является приведенный момент силы тяжести груза G:

где g - ускорение силы тяжести; т - масса груза.
Сила тяжести как при подъеме, так и при спуске груза направлена в одну сторону - в сторону спуска и неизменна по значению. Соответственно механическая характеристика исполнительного механизма w=f(Mс) в этом случае имеет вид прямой Мс=const (рис.1.3,а). Момент Mс в соответствии с (1.15) зависит от массы поднимаемого или опускаемого груза и может изменяться в пределах от Mс=0 (G=0) до Mс=Мс ном, соответствующего номинальной грузоподъемности (G=Gном).
Более широкие пределы изменения активной нагрузки характерны для уравновешенных подъемных механизмов. На рис.1.3,б показаны упрощенная схема такого механизма и соответствующие зависимости w=f(Mс) В данном случае:
M=(G1-G2)·R=g·(m-m2)·R. (1.16)
Очевидно, что в таком механизме при G2=const знак нагрузки электропривода при данном направлении скорости будет зависеть от массы m1 поднимаемого груза G1. При m1=m]HOM МС=МСном>0, так как G1>G2. При том же направлении скорости w>0 в случае m1=0 знак нагрузки в соответствии с (1.14) изменяется. Физически это означает, что по мере уменьшения массы груза m1 тормозной момент нагрузки электропривода уменьшается, при G1=G2 становится равным нулю и при дальнейшем уменьшении m1(G1>G2) двигатель должен перейти в тормозной режим, подтормаживая опускающийся груз G2, (рис.1.3,б). При изменении знака скорости w<0 (спуск груза G1) при m1=m1ном двигатель должен работать в тормозном режиме, опуская груз G1, а при m1=0 - в двигательном режиме, поднимая груз G2.
Реактивными силами и моментами называются силы и моменты сопротивления движению, возникающие как реакция на активный движущий момент, развиваемый двигателем, либо любой другой активный движущий момент, например обусловленный силой тяжести или силой инерции. Эти нагрузки всегда действуют в направлении, противоположном движению электропривода, и изменяют свое направление при изменении знака скорости.
Таким образом, все реактивные силы и моменты зависят от скорости. По характеру этой зависимости различают нагрузки типа сухого трения, типа вязкого трения и вентиляторного типа.
Силы и моменты сухого трения неизменны по модулю, но скачком изменяют свой знак при изменении знака скорости
Мс=|Mc| sign w. (1.17)
Характеристика w=f(Mс) для нагрузки типа сухого трения показана на рис.1.4,a. В реальных механизмах эта характеристика может иметь более сложный вид из-за того, что в момент трогания силы трения могут превышать их значения при движении. Эта особенность реальных сил и моментов сухого трения отмечена на рис.1.4,a штриховыми линиями и значениями момента трогания ±Мс тр.
Реактивные нагрузки, возникающие при различных технологических процессах обработки, могут иметь одно направление, скачком изменяя свое значение до нуля при изменении знака скорости. Примером может служить показанная на рис.1.4,б зависимость момента резания от скорости при обработке изделия резцом, как схематически это показано на рисунке. Значение статического момента при этом пропорционально усилию резания FZ.

где Rи - радиус изделия.
Силы и моменты вязкого трения линейно зависят от скорости:
Mс=bвт·w, (1.18)
где bвт - коэффициент пропорциональности (рис.1.5,a).
Нагрузка электропривода типа вязкого трения (1.18) на практике встречается редко, чаще всего ее можно наблюдать в виде слабой линейной составляющей в нагрузке типа сухого трения. Существенное влияние на динамические процессы в механической системе оказывают силы внутреннего вязкого трения, пропорциональные скорости деформации валов, канатов, муфт и других элементов. Момент внутреннего вязкого трения можно записать в виде (см. рис 1.2,б)
Mвт=bвт(w1-w2) (1.19)
где w1 и w2 - скорости на входе и выходе деформируемого элемента;
bвт - коэффициент пропорциональности.
По характеру влияния на механические колебания в механике все силы и моменты делятся на консервативные и диссипативные.

Mс=bмехw" (1.20)
При n=2 нагрузка называется вентиляторной (рис.1.5,б). Такой зависимостью нагрузки от скорости обладают центробежные вентиляторы. Для ряда механизмов показатель степени n>2; например такую характеристику имеют центробежные насосы, работающие на противодавление.
Существенное влияние на динамические процессы оказывают нагрузки, являющиеся периодической функцией угла поворота рабочего органа механизма. В приведенной схеме они зависят от утла поворота двигателя, например
Mc=Mmax Sin w. (1.21)
Причиной возникновения таких нагрузок являются особенности технологического процесса. Их появление можно представить себе, если в механической схеме резания, приведенной на рис.1.4,б, предположить, что заготовка имеет в сечении овальную форму. Появление периодических нагрузок могут вызывать нелинейные кинематические связи типа кривошипно-шатунных, кулисных и других механизмов, у которых периодической функцией угла поворота двигателя является радиус приведения r1j.
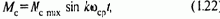 |
Во всех случаях, когда скорость двигателя при работе с такими нагрузками изменяется мало и приближенно может быть принята постоянной, для упрощения анализа периодические нагрузки рассматривают как функции времени:
где wсp - средняя за период колебаний нагрузки скорость электропривода; k - коэффициент пропорциональности, связывающий частоту колебаний нагрузки с угловой скоростью двигателя.
Нагрузки реальных электроприводов обычно содержат в качестве составляющих рассмотренные типовые нагрузки. Так, в нагрузке электропривода реальной подъемной лебедки, кроме показанной на рис.1.3,а, активной составляющей, содержится момент потерь в двигателе и передачах, который имеет вид момента сухого трения со слабой вентиляторной составляющей, обусловленной наличием самовентиляции двигателя.
При вычислении приведенного статического момента Мс формулы (1.13) и (1.14) удобны для использования в тех случаях, когда все действующие в механизме силы и моменты определены. Обычно потери на трение в механизме неизвестны, и для их учета используется КПД механизма
hмех=h1·h2·h3….,
где h1, h2, h3 - КПД элементов кинематической цепи.
 |
Если известен полезный момент нагрузки механизма Mмех, то для прямого направления энергии приведенный к валу двигателя момент статической нагрузки может быть определен из равенства
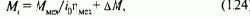 |
Следовательно,
где DM - момент механических потерь в двигателе; i0=w1/wмех=i1i2i3…- общее передаточное число от двигателя к рабочему органу механизма. При обратном направлении потока энергии, когда нагрузка является активной, движущей и двигатель должен работать в тормозном режиме, уравнение баланса мощностей с помощью КПД передач можно записать так:

В этом случае

Момент механических потерь в двигателе невелик, составляет 1-5% номинального момента двигателя, причем большие значения его соответствуют двигателям небольшой мощности. Если значение DM определить трудно, его можно ориентировочно оценить по этим данным. Во многих практических случаях в (1.24) и (1.26) полагают DM=0, так как точность определения момента Mмех невелика, и он рассчитывается с некоторым запасом, при этом формулы приведения момента статической нагрузки к валу двигателя принимают вид:
для прямого направления передачи энергии (двигательный режим работы двигателя)
 |
для обратного (тормозной режим работы двигателя)
 |
Если рабочий орган движется поступательно, уравнение баланса мощностей при прямом направлении потока энергии, принимая DМ=0, можно записать так:
 |
Откуда
Соответственно для обратного направления потока механической энергии

Необходимо иметь в виду, что КПД передач зависит от нагрузки, а для червячного зацепления - и от направления передачи энергии, поэтому при расчетах для правильного определения Мс следует использовать соответствующие зависимости hмех от полезной нагрузки передач.
Точный останов электропривода
Рассмотрим задачу точного позиционирования рабочего органа механизма в заданных точках пути по сигналам путевых датчиков, или, как ее называют иначе, задачу автоматического точного останова электропривода. Эта задача сводится к автоматическому отключению двигателя и наложению механического тормоза в такой точке пути, из которой электропривод за время торможения, двигаясь по инерции, перемещается в заданную точку пути с требуемой точностью. Процесс останова, таким образом, начинается с поступления в схему управления электроприводом импульса путевого командоаппарата на отключение двигателя и наложение механического тормоза. Если принять, что отключение двигателя и наложение механического тормоза происходят одновременно и усилие тормоза возрастает до установленного значения скачком, то весь процесс точного останова можно разделить на два этапа.
Первый этап обусловлен наличием собственного времени срабатывания аппаратуры ta в схеме управления электроприводом. Вследствие возникающего запаздывания в течение времени ta двигатель не отключается от сети, и электропривод продолжает движение со скоростью wнач, с которой он подошел к датчику точного останова, и проходит путь
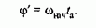
По истечении времени срабатывания аппаратуры двигатель отключается от сети, и накладывается механический тормоз. Наступает второй этап процесса останова, во время которого запасенная во всех движущихся массах системы кинетическая энергия расходуется на совершение работы по преодолению сил статического сопротивления движению на проходимом при этом пути ф":
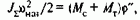
где Мт - момент механического тормоза. Откуда

На первом этапе скорость w=wнач=const, на втором она изменяется в зависимости от пути по закону
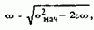
где e=(Мс+МТ)/JS- ускорение электропривода на втором этапе.
Зависимость w=f(ф) при установке датчика точного останова (ДТО) в точке ф=0 и некоторой начальной скорости wнач
показана на рис.9.1 (кривая 1). Так как все параметры, определяющие по (9.1) путь, проходимый электроприводом в процессе точного останова, при работе электропривода не остаются постоянными, абсолютно точный останов невозможен.
Так как после срабатывания ДТО движение системы является неуправляемым,наибольшая неточность останова зависит только от пределов изменения параметров, входящих в (9.1). Эти пределы можно характеризовать следующими выражениями, представляющими наибольшие и наименьшие значения соответствующих переменных и параметров:

где wср, tср, JSср, Мсср, Мтср и eср - средние значения параметров; Dw, Dt, DJ, DМс, DМТ и Demax - отклонения от средних значений параметров.

f=fcp±Dfmax (9.3)
где ф - средний путь при точном останове; Dфmax- максимальная ошибка позиционирования или максимальная неточность останова.
Как показано на рис.9.1, ДТО должен устанавливаться на расстоянии ф3=фcp , там же кривые 2 и 3 дают представления о зависимостях w=f(ф) при сочетаниях параметров, соответствующих наибольшей ошибке позиционирования.

С помощью (9.2) можно определить по (9.1) наибольший путь при точном останове

и его наименьшее значение
причем в (9.4) и (9.5) обозначено Мдин.ср=Мс.ср+Мт.ср и ВМДИН.max=DМс.max+DМТ.max. Эти выражения позволяют получить среднее значение пути, проходимого электроприводом в процессе точного останова:


Максимальная неточность останова


Анализ (9.7) свидетельствует о том, что максимальная неточность останова тем больше, чем больше средний путь при останове и чем больше относительные отклонения всех факторов, от которых он зависит, от соответствующих средних значений. Так как относительные отклонения в (9.6) и (9.7) значительно меньше единицы, то можно пренебречь их произведениями и квадратами, при этом (9.7) можно с некоторым ущербом для точности представить в значительно более удобном для пользования виде:
 |
Выражение (9.8) показывает, что наиболее существенно ошибка позиционирования зависит от средней начальной скорости и от ее отклонений от среднего значения. Поэтому из (9.8) следует, что основным фактором, вызывающим неточность останова, являются изменения нагрузки электропривода, так как они непосредственно сказываются на значении динамического момента Мдин и при данной жесткости механической характеристики электропривода определяют основное отклонение начальной скорости от среднего значения, обусловленное изменениями нагрузки, Dwmax=DМсmax/b.
Изменения нагрузки в большинстве случаев связаны с одновременным изменением суммарного приведенного момента инерции электропривода JS При данных пределах изменения статической нагрузки и известных tcp и Dtmax основным средством уменьшения ошибки позиционирования является снижение средней скорости электропривода при подходе к ДТО и увеличение жесткости механической характеристики, соответствующей работе двигателя с этой пониженной скоростью. Для получения формулы, связывающей требуемую среднюю пониженную скорость и жесткость механической характеристики с допустимой неточностью останова, примем в (9.8)
Dfmax=Dfmax.доп
где Dfmax.доп – жопустимая ошибка позиционирования, определяемая технологическими требованиями к электроприводу. При этом получается квадратное уравнение

решение которого дает следующее выражение для допустимой средней остановочной скорости:

где

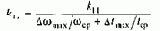


|
Рис.9.2. Механические характеристики, обеспечивающие требуемую точность позиционирования |
Рис.9.3. Зависимости w=f(ф) в процессе замедления до пониженной корости и точного останова электропривода |
Таким образом, рассматриваемый способ управления положением может обеспечить любую требуемую точность останова рабочего органа механизма в заданные позиции при правильном выборе средней остановочной скорости w и обеспечении высокой точности стабилизации этой скорости. Это означает, что требование автоматического точного останова электропривода определяет необходимый диапазон регулирования скорости электропривода D=wном/wср при заданных пределах изменения нагрузки и других возмущающих факторов.
Важным достоинством рассматриваемого способа является простота реализации, однако при высоких требованиях к точности останова и большом диапазоне регулирования, требуемом для получения этой точности, процесс точного позиционирования может при определенных условиях недопустимо затягиваться и снижать производительность позиционного механизма.
Указанные условия определяются динамическими свойствами электропривода в процессе замедления электропривода от рабочей скорости wном до пониженной остановочной скорости wср.
На рис.9.3 показаны зависимости w=f(f) при двух нагрузках электропривода Мс=Мс.max и Мс=Мс.min, соответствующие как процессу точного останова, так и предшествующему процессу замедления.
Кривые построены в предположении, что при любой нагрузке процессы замедления протекают при неизменном тормозном моменте двигателя М=Мmax=const. Тогда ускорение электропривода в этом процессе будет зависеть от нагрузки:
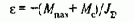
причем наименьшей нагрузке на валу Мс.min соответствует и наименьшее по абсолютному значению ускорение. При Мс=Мс.min начальная рабочая скорость при ограниченной жесткости механических характеристик электропривода максимальна: wр=wр.max, путь, проходимый электроприводом за время снижения скорости от wр.max до wнач.max при минимальном ускорении emin, также имеет максимальное значение fзам.max. Датчик импульса замедления (ДИЗ), дающий команду на замедление, устанавливается от ДТО на расстоянии 1,1·фзам.max, поэтому, как показано на рис.9.3, при Мс=Мс.min электропривод на пониженной скорости wнач.max проходит весьма небольшой отрезок пути и время дотягивания к ДТО невелико. При М=Мс.max, wр=wр.min соответственно fзам=fзам.min<<1,1фзам.max Как следствие большой отрезок пути Dфзам=1,1фзам.max-фзам.max электропривод проходит на пониженной скорости wнач.min, время дотягивания при wнач.min<<wр.min оказывается значительным и соизмеримым с общим временем, требующимся для перемещения механизма из исходного рабочего положения в заданное.
Рассматривая рис.9.3, можно заключить, что время дотягивания при любых нагрузках может быть сведено к минимуму, если устранить статическую ошибку регулирования скорости и сформировать стабильную зависимость w=f(t) в процессе замедления, инвариантную относительно нагрузки.Поэтому при большом диапазоне регулирования скорости, требуемом по условиям точного останова, возникает необходимость использования замкнутых систем регулирования скорости в системе УП-Д с достаточно высокими показателями качества и точности регулирования как в статических, так и в динамических режимах.
Однако даже при применении этой совершенной системы, с точки зрения регулирования положения, электропривод при рассмотренном способе точного позиционирования ведет себя как разомкнутая система, в которой изменения всех факторов, влияющих на путь, проходимый при точном останове, непосредственно сказываются на достигаемой точности, а небольшая нестабильность кривой изменения скорости при замедлении может существенно уменьшать быстродействие. Поэтому в наиболее сложных случаях электроприводы позиционных механизмов по системе УП-Д включаются в замкнутую систему автоматического регулирования положения по отклонению.
Уравнения движения электропривода
Механическая часть электропривода представляет собой систему твердых тел, на движение которых наложены ограничения, определяемые механическими связями Уравнения механических связей устанавливают соотношения между перемещениями в системе, а в тех случаях, когда задаются соотношения между скоростями ее элементов, соответствующие уравнения связей обычно интегрируются В механике такие связи называются голономными В системах с голономными связями число независимых переменных - обобщенных координат, определяющих положение системы, - равно числу степеней свободы системы Известно, что наиболее общей формой записи дифференциальных уравнений движения таких систем являются уравнения движения в обобщенных координатах (уравнения Лагранжа)

 |
где WK - запас кинетической энергии системы, выраженный через обобщенные координаты qi и обобщенные скорости

где L - функция Лагранжа, Q'i - обобщенная сила, определяемая суммой элементарных работ dA, всех внешних сил на возможном перемещении dqi. Функция Лагранжа представляет собой разность кинетической WK и потенциальной Wп энергий системы, выраженных через обобщенные координаты qi и обобщенные скорости


Уравнения Лагранжа дают единый и достаточно простой метод математического описания динамических процессов в механической части привода; их число определяется только числом степеней свободы системы.
В качестве обобщенных координат могут быть приняты как различные угловые, так и линейные перемещения в системе Поэтому при математическом описании динамики механической части привода с помощью уравнений Лагранжа предварительного приведения ее элементов к одной скорости не требуется. Однако, как было отмечено, до выполнения операции приведения в большинстве случаев невозможно количественно сопоставлять между собой различные массы системы и жесткости связей между ними, следовательно, невозможно выделить главные массы и главные упругие связи, определяющие минимальное число степеней свободы системы, подлежащее учету при проектировании.
Поэтому составление приведенных расчетных механических схем и их возможное упрощение являются первым важным этапом расчета сложных электромеханических систем электропривода независимо от способа получения их математического описания.
Получим уравнения движения, соответствующие обобщенным расчетным механическим схемам электропривода, представленным на рис.1.2. В трехмассовой упругой системе обобщенными координатами являются угловые перемещения масс f1, f2, f3, им соответствуют обобщенные скорости w1, w2 и w3. Функция Лагранжа имеет вид:
 |
Для определения обобщенной силы Q'1 необходимо вычислить элементарную работу всех приложенных к первой массе моментов на возможном перемещении
 |
Следовательно,
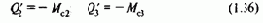 |
Аналогично определяются две другие обобщенные силы:
 |
Подставляя (1.34) в (1.32) и учитывая (1.35) и (1.36), получаем следующую систему уравнений движения:
В (1.37) пропорциональные деформациям упругих связей моменты являются моментами упругого взаимодействия между движущимися массами системы:

С учетом (1.38) систему уравнений движения можно представить в виде

Рассматривая (1.39), можно установить, что уравнения движения приведенных масс электропривода однотипны. Они отражают физический закон (второй закон Ньютона), в соответствии с которым ускорение твердого тела пропорционально сумме всех приложенных к нему моментов (или сил), включая моменты и силы, обусловленные упругим взаимодействием с другими твердыми телами системы.
Очевидно, повторять вывод уравнений движения вновь, переходя к рассмотрению двухмассовой упругой системы, нет необходимости. Движение двухмассовой системы описывается системой (1.39) при J3=0 и М23=0
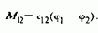 |


Отличием ее от схемы на рис.1.2,б является равенство скоростей масс w1=w2=wi, при этом в соответствии со вторым уравнением системы (1.40)

Уравнение (1.41) характеризует нагрузку жесткой механической связи при работе электропривода. Подставив это выражение в первое уравнение системы (1.40), получим
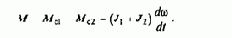
Следовательно, с учетом обозначений на рис.1.2,в МС=МС1+Мс2; JS=J1+J2 Уравнение движения электропривода имеет вид

Это уравнение иногда называют основным уравнением движения электропривода. Действительно, значение его для анализа физических процессов в электроприводе исключительно велико. Как будет показано далее, оно правильно описывает движение механической части электропривода в среднем. Поэтому с его помощью можно по известному электромагнитному моменту двигателя и значениям Мс и JS оценить среднее значение ускорения электропривода, предсказать время, за которое двигатель достигнет заданной скорости, и решить многие другие практические вопросы даже в тех случаях, когда влияние упругих связей в системе существенно.


где Rk - радиус кривошипа.
Имея в виду механизмы, аналогичные показанному на рис.1.10, рассмотрим двухмассовую систему, первая масса которой вращается со скоростью двигателя w и представляет собой суммарный приведенный к валу двигателя момент инерции всех жестко и линейно связанных вращающихся элементов J1 а вторая масса движется с линейной скоростью v и представляет собой суммарную массу т элементов, жестко и линейно связанных с рабочим органом механизма. Связь между скоростями w и v нелинейная, причем r = r(f). Для получения уравнения движения такой системы без учета упругих связей воспользуемся уравнением Лагранжа (1.31), приняв в качестве обобщенной координаты угол ф.
Вначале определим обобщенную силу:
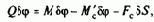
где Мс' - суммарный момент сопротивления от сил, воздействующих на линейно связанные с двигателем массы, приведенный к валу двигателя; Fc - результирующая всех сил, приложенных к рабочему органу механизма и линейно связанным с ним элементам; dS - возможное бесконечно малое перемещение массы т. Следовательно,

где r(f)=dS/df - радиус приведения
 |
При наличии нелинейной механической связи рассматриваемого типа момент статической нагрузки механизма содержит пульсирующую составляющую нагрузки, изменяющуюся в функции угла поворота f:
 |
Запас кинетической энергии системы
здесь JS(f)=J1+mr2(f) - суммарный приведенный к валу двигателя момент инерции системы.
 |
В применении к данному случаю левая часть уравнения (1.31) записывается так:
Таким образом, в рассматриваемом случае уравнение движения жесткого приведенного звена имеет вид

Рассматривая (1.45), нетрудно установить, что при наличии нелинейных механических связей уравнение движения электропривода существенно усложняется, так как становится нелинейным, содержит переменные коэффициенты, зависящие от углового перемещения ротора двигателя, и момент нагрузки, являющийся периодической функцией угла поворота. Сравнив это уравнение с основным уравнением движения (1.42), можно убедиться, что использовать основные уравнение движения электропривода допустимо лишь при постоянстве момента инерции JS=const.
В случаях, когда момент инерции при работе электропривода изменяется из-за внешних воздействий, вне связи с собственным движением, уравнение движения электропривода принимает несколько иной вид Такие условия возникают при работе машин, в которых перемещение рабочего органа по пространственным траекториям осуществляется несколькими индивидуальными электроприводами, предусмотренными для каждой координаты перемещения (экскаваторы, краны, роботы и т.п.). Например, момент инерции электропривода поворота робота зависит от вылета схвата относительно оси вращения. Изменения вылета схвата не зависят от работы электропривода поворота, они определяются движением электропривода изменения вылета.
В подобных случаях приведенный момент инерции электропривода поворота следует полагать независимой функцией времени JS(t). Соответственно, левая часть
 |
уравнения (1.31) запишется так:
а уравнение движения электропривода примет вид:
 |
Функции JS(t) и Mc(t) при этом следует определить путем анализа движения электропривода, вызывающего изменения момента инерции и нагрузки, в рассматриваемом примере это электропривод механизма изменения вылета схвата.
Полученные математические описания динамических процессов в механической части электропривода, представляемой обобщенными схемами, позволяют анализировать возможные режимы движения электропривода. Условием динамического процесса в системе, описываемой (1.42), является dw/dt¹0, т.е. наличие изменений скорости электропривода. Для анализа статических режимов работы электропривода необходимо положить dw/dt=0. Соответственно уравнение статического режима работы электропривода с жесткими и линейными механическими связями имеет вид
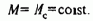
Если при движении М¹Мс, dw/dt¹0, то имеет место или динамический переходный процесс, или установившийся динамический процесс. Последнее соответствует случаю, когда приложенные к системе моменты содержат периодическую составляющую, которая после переходного процесса определяет принужденное движение системы с периодически изменяющейся скоростью.
В механических системах с нелинейными кинематическими связями (рис.1.10) в соответствии с (1.45) статические режимы работы отсутствуют. Если dw/dt=0 и w=const, в таких системах имеет место установившийся динамический процесс движения. Он обусловлен тем, что массы, движущиеся линейно, совершают принужденное возвратно-поступательное движение, и их скорость и ускорение являются переменными величинами.
С энергетической точки зрения режимы работы электропривода разделяются на двигательные и тормозные, отличающиеся направлением потока энергии через механические передачи привода (см. §1.2). Двигательный режим соответствует прямому направлению передачи механической энергии, вырабатываемой двигателем, к рабочему органу механизма.
Этот режим обычно является основным для проектирования механического оборудования, в частности редукторов. Однако при работе электропривода достаточно часто складываются условия для обратной передачи механической энергии от рабочего органа механизма к двигателю, который при этом должен работать в тормозном режиме. В частности, для электроприводов с активной нагрузкой двигательный и тормозной режимы работы вероятны практически в равной степени. Тормозные режимы работы электропривода возникают также в переходных процессах замедления системы, в которых освобождающаяся кинетическая энергия может поступать от соответствующих масс к двигателю.
Изложенные положения позволяют сформулировать правило знаков момента двигателя, которое следует иметь в виду при использовании полученных уравнений движения. При прямом направлении передачи механической мощности Р=Мw ее знак положителен, следовательно, движущие моменты двигателя должны иметь знак, совпадающий со знаком скорости. В тормозном режиме Р<О, поэтому тормозные моменты двигателя должны иметь знак, противоположный знаку скорости.
При записи уравнений движения были учтены направления моментов, показанные на обобщенных расчетных схемах, в частности на рис.1.2,в. Поэтому правило знаков для моментов статической нагрузки другое: тормозные моменты нагрузки должны иметь знак, совпадающий со знаком скорости, а движущие активные нагрузки - знак, противоположный знаку скорости.
1.5. Механическая часть электропривода как объект управления
Полученные уравнения движения позволяют проанализировать динамические особенности механической части электропривода как объекта управления, пользуясь методами теории автоматического управления. Основой для анализа являются структурные схемы, вид которых определяется принятой расчетной схемой механической части.
Получим структурные схемы для расчетных схем, представленных на рис.1.2, с их помощью проведем анализ свойств механической части электропривода и оценим погрешности, вносимые пренебрежением упругими механическими связями.
 |
Для получения структурной схемы трехмассовой упругой механической системы продифференцируем (1.38):
 |
Далее положим в (1.39) и (1.46) d/dt =p, получим

Напомним читателю известный из теории автоматического регулирования простейший способ преобразования структурных схем и получения передаточных функций для замкнутых обратными связями систем, который при необходимости используется в дальнейшем изложении. На рис.1.11,б представлен узел структурной схемы, в котором выделена передаточная функция Wпр(р), соответствующая прямой передаче сигнала, и передаточная функция Woбp(p) обратной связи. Передаточная функция замкнутого контура
 |
Путем преобразований структуры (рис.1.11,о) с помощью формулы (1.48), получим передаточную функцию механической части по управляющему воздействию при выходной переменной w1(р):
Характеристическое уравнение запишем в виде
 |
Решив биквадратное уравнение, получим корни характеристического уравнения системы:

где
Анализ корней показывает, что при всех реальных сочетаниях параметров подкоренные выражения представляют собой действительные положительные числа. Следовательно, р1=0; р23=±jW1;p45=±jW2.
Корни характеристического уравнения свидетельствуют о том, что система может быть представлена в виде последовательного соединения интегрирующего звена и двух консервативных колебательных звеньев с резонансными частотами колебаний W1 и W2.
При изменении момента М(р) скачком в системе могут возникать незатухающие колебания с частотами W1 и W2, а когда частота возмущающих воздействий совпадает с одной из этих частот, в системе развивается недемпфированный резонанс, при котором амплитуды колебаний теоретически могут возрастать до бесконечности. Реально в системе присутствуют диссипативные силы, которые демпфируют колебания, ограничивая резонансные амплитуды большими, но конечными значениями.
Более детальный анализ свойств упругих механических систем можно провести на основе двухмассовой расчетной схемы, структура которой представлена на рис.1.12,а. Она составлена на основе (1.47) при М23=0, Mc3=0 и J3=0. Для исследования свойств этой системы как объекта управления примем возмущения Мс1=Мс2=0 и выполним показанные на рис.1.12,б-г преобразования ее структуры. Прежде всего перенесем внутреннюю связь по упругому моменту на выход системы, как показано на рис.1.12,б. Эта операция позволит с помощью (1.48) определить передаточную функцию, связывающую выходную координату со скоростью w1:

Далее находим передаточную функцию двухмассовой системы по управлению при выходной переменной w1 аналогично рассмотренной выше для трехмассовой системы (1.49). В соответствии со схемой рис.1.12,б передаточная функция прямого канала
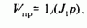
 |
а обратной связи
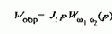
 |
Следовательно, искомая передаточная функция с учетом (1.50) определяется так:
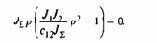 |
Характеристическое уравнение системы
 |
Корни характеристического уравнения
где W12 - резонансная частота двухмассовой упругой системы.
Сравнение (1.52) с корнями (1.49) показывает, что при переходе от трехмассовой упругой системы к двухмассовой выявляется только одна частота W12, на которой возможно проявление механического резонанса. Однако, если при этом значение W12 оказывается достаточно близким к одной из парциальных частот исходной системы W1 или W2, можно полагать, что двухмассовая система правильно отражает главные особенности механической части электропривода.
Для удобства анализа введем следующие обобщенные параметры двухмассовой упругой системы:
g=(J1+ J2)/J1=JS/J1 - соотношение масс;
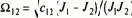
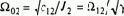
 |
С учетом этих обозначений (1.50) и (1.51) могут быть представлены в виде:
 |
Полученные соотношения (1.53) и (1.54) позволяют представить механическую часть электропривода как объект управления в виде трех звеньев, показанных на рис.1.12,в. С помощью этой схемы нетрудно записать и передаточную функцию системы по управляющему воздействию при выходной переменной w2:
Передаточной функции (1.55) соответствует структурная схема объекта, представленная на рис.1.12,г. Для анализа свойств системы воспользуемся частотным методом теории управления. Уравнение амплитудно-фазовой характеристики (АФХ) получим, подставив в (1.54) р=jW:
 |
где Aw1(W) - амплитудно-частотная характеристика (АЧХ); Yw1(W) - фазо-частотная характеристика (ФЧХ) объекта при выходной переменной w1.
Прежде чем перейти к построению логарифмических частотных характеристик, необходимо обратить внимание на то, что при анализе механической и электрической частей системы электропривода здесь и в дальнейшем рассматриваются их передаточные функции, в которых выходная и входная переменные чаще всего имеют различные единицы измерения В этих случаях W(jW) представляет собой не комплексный коэффициент усиления, а комплексный коэффициент передачи, имеющий определенную единицу измерения В частности, в (1.56) его единица 1/(Н м·с), такую же размерность имеет величина Аw1(W).
При необходимости все дифференциальные уравнения и передаточные функции системы могут быть представлены в относительных единицах. Эта возможность используется при расчетах и исследованиях электроприводов.
В данном курсе, чтобы не осложнять понимание физического смысла явлений и параметров, представление переменных в относительных единицах, как правило, не используется. При этом для выражения АЧХ в логарифмическом масштабе единицы амплитуд опускаются, что соответствует относительным их значениям при базовом значении, равном единице измерения.
Асимптотические логарифмические АЧХ (ЛАЧХ) могут быть построены непосредственно по полученным передаточным функциям системы. В частности, в соответствии с (1.54) система может быть представлена последовательным соединением интегрирующего звена, форсирующего звена второго порядка с частотой сопряжения Wc1=W12/



Проанализируем основные свойства механической части, воспользовавшись ее структурой, представленной на рис.1.12,в, и частотными характеристиками, изображенными на рис.1.13 При этом обратим внимание на различия во влиянии упругости на движение первой и второй масс. Движение первой массы при небольших частотах колебаний управляющего воздействия М в соответствии с (1.54) и рис.1.13,а определяется суммарным моментом инерции электропривода JS, причем механическая часть ведет себя как интегрирующее звено. В частности, при М=const скорость w1 изменяется по линейному закону, на который накладываются колебания, обусловленные упругой связью. Иными словами, интегрирующее звено в структуре на рис.1.12,б характеризует условия движения механической части в среднем.
При приближении частоты колебаний момента к резонансной W12 амплитуды колебаний скорости w1 возрастают и при W1=W12 стремятся к бесконечности. Однако проявления резонанса существенно зависят от параметров механической части в связи с наличием в числителе передаточной функции Ww1 форсирующего звена второго порядка. Можно выявить условия, при выполнении которых влияние упругости на движение первой массы будет незначительным.
Во-первых, из (1.54) непосредственно следует, что если механизм обладает небольшой инерцией (J2<<J1, g®1), то движение первой массы близко к движению, определяемому интегрирующим звеном Wи=JS/p. Во-вторых, из (1.56) видно, что при W12®¥ в области малых и средних частот движение первой массы определяется тем же интегрирующим звеном. Отсюда вытекает важный практический вывод. Если при синтезе электропривода используются обратные связи только по переменным двигателя, то при J2<<J1 или W12>>Wc где Wс - частота среза желаемой ЛАЧХ разомкнутого контура регулирования, механическую часть электропривода можно представить жестким механическим звеном, не учитывая влияния упругостей.
В соответствии с (1.55) и рис.1.13,б колебательность второй массы выше, чем первой. В низкочастотной области асимптоты ЛАЧХ Lw1 и Lw2 совпадают, так как в среднем движение второй массы также определяется интегрирующим звеном Wи=JS/p.
Однако при W> W2 наклон высокочастотной асимптоты Lw2 составляет -60 дБ/дек, и нет факторов, которые ослабляли бы развитие резонансных колебаний при любых g.
|
Рис 1.14 Структурная схема механической части с жесткими механическими связями. |

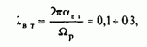
где aвт и Wp=W12 - коэффициент затухания и резонансная частота колебаний с учетом влияния внутренних диссипативных сил.
Учет естественного демпфирования существенно не сказывается на форме ЛАЧХ и ЛФЧХ системы, однако, ограничивает резонансный пик конечными значениями, как показано штриховой кривой 1 на рис.1.13,а, и несколько сглаживает фазочастотную характеристику (штриховая кривая 2 на том же рисунке). Аналогичные изменения, вносимые естественным демпфированием в частотные характеристики на рис.1 13,б, показаны штриховыми кривыми, обозначенными соответственно 1' и 2'.
Сочетания параметров, при которых J2<<J1 или W2®¥, Достаточно распространены, поэтому в дальнейшем изложении во всех случаях, когда это допустимо, используется представление механической части электропривода в виде жесткого приведенного звена. Уравнению движения (1.42) для этого случая при р=d/dt соответствует структурная схема, представленная на рис.1.14. Она совпадает с входным звеном в рассмотренной выше структуре рис.1.12,в, и частотные характеристики жесткой механической части электропривода в низкочастотной области не отличаются от приведенных на рис.1.13.
Устойчивость статического режима работы электропривода
Статическому режиму работы соответствует движение всех элементов электромеханической системы с постоянной и одинаковой приведенной скоростью. Этот режим наступает после затухания свободных составляющих переходного процесса, вызванного изменением управляющего или возмущающих воздействий, и характеризуется равенством электромагнитного момента двигателя суммарному моменту нагрузки.
Последнее следует непосредственно из уравнений движения электропривода, если положить в них р=0. Так, для электромеханической системы с упругой связью, положив p=0 в (4.5), получим

откуда
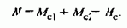
Для одномассовой расчетной механической схемы, приняв р=0 в уравнении движения электропривода
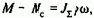
получим тот же результат: М=Мс.
В гл.1 было показано, что в общем случае момент нагрузки в той или иной степени зависит от скорости. Зависимость Mc=f(w) или w=f(Мс) является механической характеристикой исполнительного механизма, а так как момент двигателя также в соответствии с его механической характеристикой зависит от скорости, условие статического режима можно записать в таком виде:

где wс - скорость электропривода в статическом режиме.

Графически условие (4.28) определяется точкой пересечения механической характеристики двигателя w=f(М) с механической характеристикой исполнительного механизма w=f(Мс) (рис.4.13). На этом рисунке в качестве примера представлены механические характеристики 1 и 2 асинхронного двигателя для двух направлений вращения его магнитного поля, а также ряд механических характеристик различных исполнительных механизмов (3-5). Характеристика 3, как было показано в гл.1, соответствует механизму с активной полезной нагрузкой, например подъемной лебедке. При w>0, что соответствует подъему груза, пересечение этой характеристики с механической характеристикой двигателя дает точку статического режима wc1, в которой двигатель, работая в двигательном режиме, преодолевает активный полезный момент и реактивный момент механических потерь.
При противоположном направлении вращения (w<0) характеристика 3, пересекаясь с характеристикой двигателя 2, дает точку статического режима wс2. Здесь двигатель работает в режиме рекуперативного торможения и его тормозной момент совместно с реактивным моментом механических потерь уравновешивает движущий момент полезной нагрузки.
Характеристика 4 пересекается с механической характеристикой двигателя в двух точках, чему соответствуют две скорости wс3 и wс4, при которых выполняется условие статического равновесия (4.28). Однако устойчивым это равновесие является только при скорости wс3. Незначительное отклонение скорости от wс4 вниз дает уменьшение момента двигателя, и в соответствии с (4.27) появляется динамический момент отрицательного знака, вызывающий дальнейшее снижение скорости. Аналогичное отклонение скорости вверх от wс4
приводит, напротив, к увеличению момента двигателя и появлению положительного динамического момента, что вызывает дальнейшее возрастание скорости вплоть до w=wс3. При этом значении скорости динамические моменты, возникающие при любом малом отклонении скорости, направлены на уменьшение возникшего отклонения скорости и возвращают электропривод в точку устойчивого равновесия. Увеличение момента нагрузки вплоть до значения, соответствующего критическому моменту двигателя, приводит к слиянию точек устойчивого и неустойчивого равновесия в одну точку неустойчивого равновесия w=wк=w0(1-sk), поэтому участок механической характеристики асинхронного двигателя при w<wк обычно называют неустойчивым.
Условия возникновения динамического момента при отклонениях от точки статического равновесия зависят как от формы характеристики двигателя, так и от вида характеристики исполнительного механизма. На рис.4.13 показана механическая характеристика вентилятора 5, пересекающая характеристику двигателя в точке wс4. Путем аналогичного анализа можно установить, что благодаря более значительным изменениям момента нагрузки, чем момента двигателя, возникающие при отклонениях скорости от wс4 динамические моменты возвращают систему к скорости wс4 и равновесие становится устойчивым.
Из изложенного следует, что при Мс=const устойчивость статического режима работы зависит от знака жесткости статической механической характеристики двигателя. Условие устойчивости: bст=dM/dw<0. Если момент механизма зависит от скорости, то его механическая характеристика также обладает определенной жесткостью bмех=dMc/dw, при этом условие статической устойчивости принимает вид

Следует иметь в виду, что приведенные рассуждения и полученные условия устойчивости статического режима работы справедливы только для электроприводов, у которых статическая и динамическая механические характеристики совпадают, например, в случае, когда Tэ=0. В общем случае устойчивость статического режима работы электропривода определяется динамической жесткостью механической характеристики и параметрами механической части привода, поэтому она должна устанавливаться на основании анализа корней характеристического уравнения системы или частотными методами теории автоматического регулирования.
Влияние отрицательной связи по моменту (току) на динамику упругой электромеханической системы
Структурная схема упругой электромеханической системы, замкнутой отрицательной обратной связью по моменту (или току) двигателя, приведена на рис.7.22,а. В результате структурных преобразований эту схему можно привести к виду, представленному на рис.7.22,б. Сравнивая преобразованную схему со структурной схемой обобщенной разомкнутой упругой электромеханической системы на рис.6.15,а, можно установить, что введение обратной связи по моменту видоизменяет передаточную функцию динамической жесткости механической характеристики При данной механической части динамика упругой электромеханической системы полностью определяется частотными характеристиками динамической жесткости, а изменения, вносимые обратной связью по моменту, выявляются путем анализа изменений в указанных характеристиках.
В гл.4 было установлено, что электропривод с линейной механической характеристикой при определенных сочетаниях параметров оказывает на возникающие в механической части упругие колебания сильное демпфирующее действие. Был выполнен анализ этого влияния для системы, имеющей передаточную функцию динамической жесткости
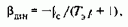
и установлены оптимальные сочетания параметров, обеспечивающие минимум колебательности электромеханической системы. Передаточная функция динамической жесткости в системе, замкнутой отрицательной связью по моменту, определяется выражением (7.28):

Изменения, вносимые обратной связью по моменту, при Тп»0 наглядно показаны на рис.7.11,а, а при Тп>>ТЭ - на рис.7.11,б.
При безынерционном преобразователе (Tп=0) отрицательная обратная связь по моменту эквивалентна введению дополнительных сопротивлений в силовую цепь двигателя. Если в разомкнутой системе жесткость естественной механической характеристики bе была выше оптимальной по критерию минимума колебательности, путем введения отрицательной связи по моменту или току можно увеличить демпфирование колебаний. Если, напротив, жесткость bе ниже оптимальной, отрицательная связь по моменту может только ухудшать демпфирование.

Во всех подобных случаях она отрицательно сказывается на колебательности процессов в механической части электропривода. При преобразователе, обладающем большой электромагнитной инерцией (ТП>>ТЭ), при определенных сочетаниях параметров высокое демпфирование сохраняется даже при абсолютно мягкой статической механической характеристике В этом можно убедиться, рассматривая рис.7.11,б: малая жесткость bзм сохраняется только при весьма низких частотах: W<1/Tп. В области средних частот инерционность преобразователя является фильтром и обратная связь по моменту проявляется слабо (bзм®bе). Если l/T'п£W12£1/Tэ и в разомкнутой системе имела место минимальная колебательность, то она может не измениться существенно и в системе, замкнутой по моменту или току.
Значение Tп' зависит от коэффициента отрицательной связи по моменту (току), поэтому наиболее благоприятные условия для сохранения демпфирующей способности при регулировании момента обеспечиваются в комбинированной системе регулирования с формирующей положительной связью по скорости. Введение критической положительной связи по скорости позволяет обеспечить высокую статическую точность регулирования, а коэффициент отрицательной связи по моменту или току может быть выбран таким, чтобы на частоте резонанса W12 динамическая жесткость была близка к естественной be.
Рассмотренные условия характерны для мощных электроприводов, выполненных по схеме Г-Д. Использование отрицательной связи по току якоря в сочетании с критической положительной связью по напряжению генератора в системе Г-Д обеспечивает благоприятные характеристики и динамические свойства многих электроприводов действующих установок в различных отраслях промышленности.
При настройке контура регулирования момента (тока) на технический оптимум в системе ТП-Д путем последовательной коррекции роль фильтра может выполнять постоянная интегрирования Тн ПИ-регулятора, но только в области высоких частот механических колебаний. При суммарной некомпенсируемой постоянной Tm<0,01 с быстродействие контура при aм=2 высоко и электромеханическая связь на частотах W12=10¸30 1/с ослабляется существенно.Уменьшить быстродействие и сохранить демпфирование можно путем выбора ам>2. Однако при этом необходимо проверить, не снижается ли при больших ам динамическая точность регулирования момента до недопустимого уровня.
В заключение отметим, что электропривод по системе ИТ-Д без обратных связей обладает свойствами практически идеального источника момента В таком электроприводе демпфирование упругих колебаний со стороны электрической части системы невозможно, так как связь электрических и механических процессов в системе отсутствует, и механические колебания не оказывают влияния на развиваемый двигателем электромагнитный момент.
